题目内容
19.函数y=$\sqrt{1-2x}$中自变量x的取值范围是x≤$\frac{1}{2}$.函数y=$\frac{1-2x}{3x-1}$,x=$\frac{1}{2}$时,y的值为0.分析 根据被开方数大于等于0列式计算即可得解;
令y=0,解方程即可.
解答 解:由题意得,1-2x≥0,
解得x≤$\frac{1}{2}$;
令y=0,则$\frac{1-2x}{3x-1}$=0,
解得x=$\frac{1}{2}$.
故答案为:x≤$\frac{1}{2}$;$\frac{1}{2}$.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.下列由左到右的变形中属于因式分解的是( )
| A. | 24x2y=3x•8xy | B. | m2-2m-3=m(m-2)-3 | C. | x2+2x+1=(x+1)2 | D. | (x+3)(x-3)=x2-9 |
4.四边形ABCD的对角线AC、BD相交于点O,下列条件中能判定它为矩形的是( )
| A. | AO=CO,BO=DO,AB=BC | B. | AO=CO,BO=DO,AB=DC | ||
| C. | AB∥CD,AD∥BC,AO=CO | D. | AO=BO=CO=DO |
11.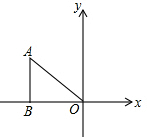 如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
 如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,1)或(2,-1) |
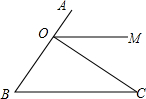 如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.
如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.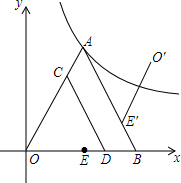 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.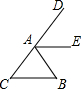 如图,已知AB=AC,AE平分∠DAB.求证:AE∥BC.
如图,已知AB=AC,AE平分∠DAB.求证:AE∥BC.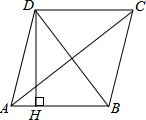 如图,四边形ABCD是菱形,AD=5,DB=6,DH⊥AB于H,则DH的长为$\frac{24}{5}$.
如图,四边形ABCD是菱形,AD=5,DB=6,DH⊥AB于H,则DH的长为$\frac{24}{5}$.