题目内容
14．
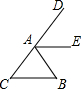如图，已知AB=AC，AE平分∠DAB．求证：AE∥BC．
分析 根据角平分线的定义得出∠DAE=∠BAE，根据等腰三角形的性质得到∠B=∠C，再利用三角形外角的性质和等量关系得到∠BAE=∠B，根据内错角相等，两直线平行证明即可求解．
解答 证明：∵AE平分∠DAB，
∴∠DAE=∠BAE，
∵AB=AC，
∴∠B=∠C，
∵∠DAB=∠B+∠C，
∴∠BAE=∠B，
∴AE∥BC．
点评 此题考查平行线的判定，关键是根据角平分线的定义、等腰三角形的性质和三角形外角的性质得出∠BAE=∠B．
练习册系列答案
相关题目
5．
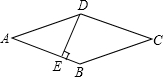如图，菱形ABCD的周长为8cm，DE⊥AB，垂足为E，若sinA=$\frac{4}{5}$，则EB的长为（ ）
如图，菱形ABCD的周长为8cm，DE⊥AB，垂足为E，若sinA=$\frac{4}{5}$，则EB的长为（ ）| A． | 0.4 | B． | 0.5 | C． | 0.6 | D． | 0.8 |
6．已知三角形的三边长为a、b、c，由下列条件能构成直角三角形的是（ ）
| A． | a2=（m-1）2，b2=4m2，c2=（m+1）2 | B． | a2=（m-1）2，b2=4m，c2=（m+1）2 | ||
| C． | a2=（m-1）2，b2=2m，c2=（m+1）2 | D． | a2=（m-1）2，b2=2m2，c2=（m+1）2 |