题目内容
16. 如图,每个小正方形的边长为1,△ABC的三个顶点都在格点(小正方形的顶点)上.
如图,每个小正方形的边长为1,△ABC的三个顶点都在格点(小正方形的顶点)上.(1)己知A(-3,2).建立平面直角坐标系并写出B、C的坐标;
(2)将△ABC先向右平移6个单位,再向上平移3个单位得△A1B1C1,画出平移后的△A1B1C1;
(3)若以A、B、C、D为顶点的四边形为平行四边形,直接写出D点的坐标.
分析 (1)根据题意建立坐标系后,即可解决问题.
(2)△ABC先向右平移6个单位,再向上平移3个单位得△A1B1C1,根据要求画出图象即可.
(3)点D为顶点的平行四边形有三个,画出图形即可解决问题.
解答 解:(1)平面直角坐标系如图所示,点B坐标(-5,1),点C坐标(-2,0).
(2)△A1B1C1坐如图所示.
(3)由图象可知点D坐标为(-6,3)或(0,1)或(-4,-1).
点评 本题考查平移-作图变换、平行四边形的性质等知识,解题的关键是学会建立平面直角坐标系,掌握图形的平移的规律,求点D坐标时不能漏解,属于中考常考题型.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
7.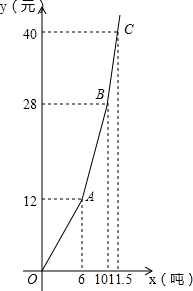 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
(1)填空
价目表
(2)若某户居民9月份用水量为9.5吨,求该用户9月份水费;
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).(1)填空
价目表
| 每月水用量 | 单价 |
| 不超出6吨的部分 | 2元/吨 |
| 超出6吨不超出10吨的部分 | 4 元/吨 |
| 超出10吨的部分 | 8元/吨 |
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
4.下列计算正确的是( )
| A. | $\sqrt{4+9}=\sqrt{4}+\sqrt{9}$ | B. | 2$\sqrt{2}-\sqrt{2}$=2 | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\frac{{\sqrt{21}}}{{\sqrt{3}}}=\sqrt{\frac{21}{3}}=\sqrt{7}$ |
11.下列命题中,是真命题的是( )
| A. | 有理数都是有限小数 | |
| B. | 同旁内角互补 | |
| C. | 函数y=$\frac{1}{\sqrt{x-3}}$自变量x的取值范围是x≥3 | |
| D. | 若甲、乙两组数据中各有20个数据,平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,方差S甲2=1.25,S乙2=0.96,则说明乙组数据比甲组数据稳定 |
8.若一次函数y=(m-3)x+5的函数值,y随x的增大而增大,则( )
| A. | m<0 | B. | m>0 | C. | m<3 | D. | m>3 |
5. 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
 如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,添加一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | AD=CB | C. | BE=DF | D. | AD∥BC |
6.下列关于图形旋转的说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | |
| B. | 对应点与旋转中心所连线段的夹角等于旋转角 | |
| C. | 旋转前后的图形全等 | |
| D. | 旋转后,图形的大小,形状与位置都发生了变化 |



