题目内容
10.已知⊙O的半径为6cm,弦AB的长为6cm,则弦AB所对的圆周角的度数为30°或150°.分析 根据弦长等于半径,得这条弦和两条半径组成了等边三角形,则弦所对的圆心角是60°,要计算它所对的圆周角,
应考虑两种情况:当圆周角的顶点在优弧上时,则根据圆周角定理,得此圆周角是30°;
当圆周角的顶点在劣弧上时,则根据圆内接四边形的对角互补,得此圆周角是150°.
解答 解:根据题意,弦AB与两半径组成等边三角形,
∴弦AB所对的圆心角=60°,
①圆周角在优弧上时,圆周角=30°,
②圆周角在劣弧上时,圆周角=180°-30°=150°.
∴圆周角的度数为30°或150°;
故答案为:30°或150°.
点评 本题考查了圆周角定理;注意:弦所对的圆周角有两种情况,且两种情况的角是互补的.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
1.若a<b,则下列各式中,错误的是( )
| A. | a-3<b-3 | B. | -a<-b | C. | -2a>-2b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |
15.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2•a3=a6 | C. | a5÷a3=a2 | D. | (a+2a)2=4a2 |
19.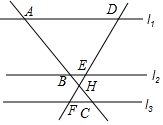 如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
 如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
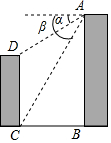 小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为20$\sqrt{3}$米.
小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为20$\sqrt{3}$米. 如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.
如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.