题目内容
2. 如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.
如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.
分析 根据三角形中位线定理、菱形的判定定理得到四边形EFGH是菱形,根据菱形的性质定理进行判断即可.
解答 解:∵E,F,G,H分别是BD,BC,AC,AD的中点,
∴EH∥AB,EH=$\frac{1}{2}$AB,GF∥AB,EH=$\frac{1}{2}$AB,GH∥CD,GH=$\frac{1}{2}$CD,
∴EH∥GF,EH=GF,
∴四边形EFGH是平行四边形,
∵AB=CD,
∴EH=GH,
∴四边形EFGH是菱形,⑤正确;④不正确;
∴EG⊥FH,①正确;
HF平分∠EHG,②正确;
∵AD与BC不平行,
∴EG≠$\frac{1}{2}$(BC-AD),④不正确,
故答案为:①②⑤.
点评 本题考查的是中点四边形的性质,掌握三角形中位线定理、菱形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
17.已知a>b,且c为非零实数,那么下列结论一定正确的是( )
| A. | ac<bc | B. | ac2<bc2 | C. | ac>bc | D. | ac2>bc2 |
7.当-4≤x≤2时,函数y=-(x+3)2+2的取值范围为( )
| A. | -23≤y≤1 | B. | -23≤y≤2 | C. | -7≤y≤1 | D. | -34≤y≤2 |
14.宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
| A. | 0.35×1010元 | B. | 3.5×108元 | C. | 3.5×109元 | D. | 35×108元 |
 用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )
用4个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )



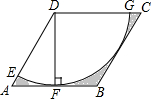 如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)
如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)