题目内容
3．下列结论正确的是（ ）| A． | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0，则a=±1 | |
| B． | 单项式-x2的系数是-1 | |
| C． | 使式子$\sqrt{x+2}$有意义的x的取值范围是x＞-2 | |
| D． | 3a2b-a2b=2 |
分析 根据各个选项中的说法，可以判断各个选项中的说法是否正确，本题得以解决．
解答 解：∵$\frac{{a}^{2}-1}{a+1}$=0，可得a=1，故选项A错误；
∵单项式-x2的系数是-1，故选项B正确；
∵要使式子$\sqrt{x+2}$有意义，可得x+2≥0，得x≥-2，故选项C错误；
∵3a2b-a2b=2a2b，故选项D错误；
故选B．
点评 本题考查分式的值为零的条件、单项式的系数、二次根式有意义的条件、合并同类项，解题的关键是明确它们各自的含义．
练习册系列答案
一线名师权威作业本系列答案
相关题目
14．下列各式正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （x+6）（x-6）=x2-6 | C． | （2x+3）2=2x2-12x+9 | D． | （2x-1）2=4x2-4x+1 |
11．下列各式运算正确的是（ ）
| A． | $\sqrt{2}•\sqrt{3}=\sqrt{5}$ | B． | （-a2b）3=-a6b3 | C． | a2•a3=a6 | D． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ |
已知⊙O，如图所示．
15．关于x的不等式（a-1）x＜a+6的解集与不等式2x＜4的解集相同，那么a的值为（ ）
| A． | 5 | B． | 8 | C． | -8 | D． | 9 |
12．下列二次根式中与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{4}$ | B． | $\sqrt{6}$ | C． | $\sqrt{8}$ | D． | $\sqrt{10}$ |
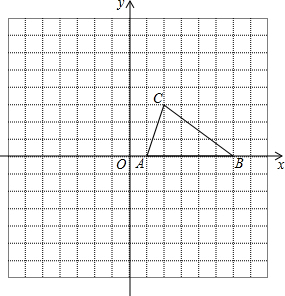如图方格纸中，已知△ABC的三个顶点的坐标分别为A（1，0）、B（6，0）、C（2，3）．