题目内容
11.下列各式运算正确的是( )| A. | $\sqrt{2}•\sqrt{3}=\sqrt{5}$ | B. | (-a2b)3=-a6b3 | C. | a2•a3=a6 | D. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ |
分析 根据二次根式的加减法则、乘法法则、幂的乘方与积的乘方法则对各选项进行逐一分析即可.
解答 解:A、$\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$≠$\sqrt{5}$,故本选项错误;
B、(-a2b)3=-a6b3,故本选项正确;
C、a2•a3=a5≠a6,故本选项错误;
D、$\sqrt{8}$-$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$≠$\sqrt{6}$,故本选项错误.
故选B.
点评 本题考查的是二次根式的加减法,熟知二次根式的加减法则、乘法法则、幂的乘方与积的乘方法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x-y)2=81 | B. | x2+y2=65 | C. | x2+y2-xy=71 | D. | x2-y2=±63 |
2.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{2\frac{1}{4}}$=1$\frac{1}{2}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\root{3}{-27}$=-9 |
6.下列各式中,运算正确的是( )
①(22a)2=4a2;
②(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2;
③(m-1)2(1-m)3=(m-1)5;
④(-a-b)2-a2=2ab+b2.
①(22a)2=4a2;
②(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2;
③(m-1)2(1-m)3=(m-1)5;
④(-a-b)2-a2=2ab+b2.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
16.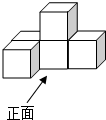 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )| A. | 左视图的面积为2 | B. | 俯视图的面积为3 | ||
| C. | 主视图的面积为4 | D. | 三种视图的面积都是4 |
3.下列结论正确的是( )
| A. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 3a2b-a2b=2 |
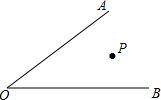 根据下列语句画图:如图,∠AOB内有一点P:
根据下列语句画图:如图,∠AOB内有一点P: