题目内容
15.关于x的不等式(a-1)x<a+6的解集与不等式2x<4的解集相同,那么a的值为( )| A. | 5 | B. | 8 | C. | -8 | D. | 9 |
分析 先求出第二个不等式的解集,再根据两个不等式的解集相同,列出方程求解即可.
解答 解:不等式2x<4的解集是x<2.
∵两不等式的解集相同,
∴关于x的不等式(a-1)x<a+6的解集为x<2,
而关于x的不等式(a-1)x<a+6的解集可表示为x<$\frac{a+6}{a-1}$,
∴$\frac{a+6}{a-1}$=2,解得a=8.
故选B.
点评 本题考查了解简单不等式的能力.解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
5.下列各式,正确的是( )
| A. | x3+x3=2x3 | B. | x3•x4=x12 | C. | (x2)3=x5 | D. | x8÷x4=x2 |
6.下列各式中,运算正确的是( )
①(22a)2=4a2;
②(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2;
③(m-1)2(1-m)3=(m-1)5;
④(-a-b)2-a2=2ab+b2.
①(22a)2=4a2;
②(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2;
③(m-1)2(1-m)3=(m-1)5;
④(-a-b)2-a2=2ab+b2.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
3.下列结论正确的是( )
| A. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 3a2b-a2b=2 |
10.下列各组数是方程组$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$的解的是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
7.下列运算正确的是( )
| A. | -$\sqrt{-25}$=5 | B. | $\root{3}{1{0}^{6}}$=102 | C. | $\sqrt{4+\frac{9}{16}}$=2$\frac{3}{4}$ | D. | $\sqrt{0.25}$=±0.5 |
4.(-0.5)-2等于( )
| A. | 1 | B. | 4 | C. | -4 | D. | 0.25 |
5.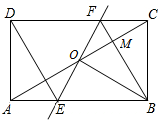 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )| A. | FB⊥OC,OM=CM | B. | △EOB≌△CMB | ||
| C. | 四边形EBFD是菱形 | D. | MB:OE=3:2 |
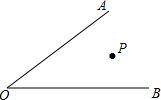 根据下列语句画图:如图,∠AOB内有一点P:
根据下列语句画图:如图,∠AOB内有一点P: