题目内容
13.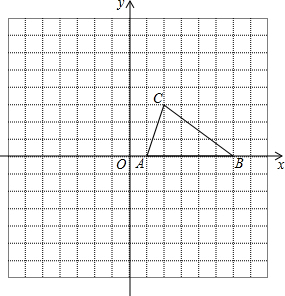 如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).
如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).(1)请直接写出点C关于y轴对称的点C1的坐标;
(2)将△ABC绕坐标点A逆时针旋转90°,画出对应的△AB2C2,直接写出点C的对应点C2的坐标;
(3)y轴上存在一点P,使PA+PC的值最小,直接写出满足PA+PC的值最小的点P坐标.
分析 (1)根据关于y轴对称的点横坐标互为相反数,纵坐标相同解答;
(2)根据网格结构找出点A、B、C绕点点A逆时针旋转90°后的图形,再根据平面直角坐标系写出点C的对应点C2的坐标即可;
(3)连接AC1交y轴于点P,则点P即为所求点.
解答  解:(1)点C(2,3)关于y轴的对称点的坐标为(-2,3);
解:(1)点C(2,3)关于y轴的对称点的坐标为(-2,3);
(2)△ABC绕坐标点A逆时针旋转90°的图形如图所示:
点C的对应点C2的坐标为(-2,1);
(3)连接AC1交y轴于点P,则点P即为所求点,点P坐标为(0,1).
点评 本题考查了利用旋转变换作图,关于x轴、y轴对称的点的坐标特征,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
3.下列结论正确的是( )
| A. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 3a2b-a2b=2 |
4.(-0.5)-2等于( )
| A. | 1 | B. | 4 | C. | -4 | D. | 0.25 |
18.下列式子中:$\sqrt{s}$、$\root{3}{5}$、0、$\sqrt{25}$、$\frac{5}{3}$、$\sqrt{a}$(a>0)二次根式的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.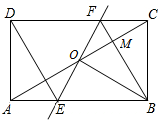 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )| A. | FB⊥OC,OM=CM | B. | △EOB≌△CMB | ||
| C. | 四边形EBFD是菱形 | D. | MB:OE=3:2 |
3.若二次根式$\sqrt{3x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x$>\frac{1}{3}$ | B. | x≠$\frac{1}{3}$ | C. | x$≥\frac{1}{3}$ | D. | x≥0 |
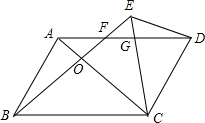 如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)
如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)