题目内容
8.阅读下面材料:在数学课上,老师提出如下问题:
如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC.
甲、乙、丙、丁四位同学的主要作法如下:
甲同学的作法:如图甲:以点B为圆心,BA长为半径画弧,交BC于点P,则点P就是所求的点.乙同学的作法:如图乙:作线段AC的垂直平分线交BC于点P,则点P就是所求的点.丙同学的作法:如图丙:以点C为圆心,CA长为半径画弧,交BC于点P,则点P就是所求的点.丁同学的作法:如图丁:作线段AB的垂直平分线交BC于点P,则点P就是所求的点.
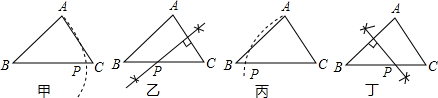
请你判断哪位同学的作法正确丁同学;
这位同学作图的依据是垂直平分线上的点到线段两端的距离相等;等量代换.
分析 分别利用线段垂直平分线的性质结合圆的性质分析得出答案.
解答 解:甲同学的作法:如图甲:以点B为圆心,BA长为半径画弧,交BC于点P,则点P就是所求的点.
无法得出AP=BP,故无法得出PA+PC=BC,故此选项错误;
乙同学的作法:如图乙:作线段AC的垂直平分线交BC于点P,则点P就是所求的点.
无法得出AP=BP,故无法得出PA+PC=BC,故此选项错误;
丙同学的作法:如图丙:以点C为圆心,CA长为半径画弧,交BC于点P,则点P就是所求的点.
无法得出AP=BP,故无法得出PA+PC=BC,故此选项错误;
丁同学的作法:如图丁:作线段AB的垂直平分线交BC于点P,则点P就是所求的点,
可得:AP=BP,则PA+PC=BC.
故答案为:丁;垂直平分线上的点到线段两端的距离相等;等量代换.
点评 此题主要考查了复杂作图,正确把握线段垂直平分线的性质是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
18.下列说法中,不正确的是( )
| A. | 2是(-2)2的算术平方根 | B. | ±2是(-2)2的平方根 | ||
| C. | -2是(-2)2的算术平方根 | D. | -2是(-2)3的立方根 |
16.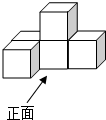 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )| A. | 左视图的面积为2 | B. | 俯视图的面积为3 | ||
| C. | 主视图的面积为4 | D. | 三种视图的面积都是4 |
3.下列结论正确的是( )
| A. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 3a2b-a2b=2 |
13.下列等式正确的是( )
| A. | $\sqrt{\frac{9}{16}}$=±$\frac{3}{4}$ | B. | $\root{3}{-9}=-3$ | C. | $\sqrt{(-\frac{1}{3})^{2}}=\frac{1}{3}$ | D. | $\sqrt{-1\frac{7}{9}}=1\frac{1}{3}$ |
17.下列式子正确的是( )
| A. | $\sqrt{8}$=±2$\sqrt{2}$ | B. | $\root{3}{-8}$=-2 | C. | $\root{3}{-8}$=-2$\sqrt{2}$ | D. | $\sqrt{-8}$=-2$\sqrt{2}$ |
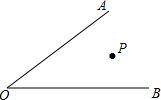 根据下列语句画图:如图,∠AOB内有一点P:
根据下列语句画图:如图,∠AOB内有一点P: