题目内容
12.下列二次根式中与$\sqrt{2}$是同类二次根式的是( )| A. | $\sqrt{4}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
分析 判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行,或直观地观察被开方数的每一个因数(或因式)的指数都小于根指数2,且被开方数中不含有分母,被开方数是多项式时要先因式分解后再观察.
解答 解:A、$\sqrt{4}$=2,与$\sqrt{2}$不是同类二次根式;
B、$\sqrt{6}$与$\sqrt{2}$不是同类二次根式;
C、$\sqrt{8}=2\sqrt{2}$与$\sqrt{2}$是同类二次根式,正确;
D、$\sqrt{10}$与$\sqrt{2}$不是同类二次根式;
故选:C.
点评 本题考查了最简二次根式的定义.在判断最简二次根式的过程中要注意:
(1)在二次根式的被开方数中,只要含有分数或小数,就不是最简二次根式;
(2)在二次根式的被开方数中的每一个因式(或因数),如果幂的指数大于或等于2,也不是最简二次根式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{2\frac{1}{4}}$=1$\frac{1}{2}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\root{3}{-27}$=-9 |
3.下列结论正确的是( )
| A. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 3a2b-a2b=2 |
7.下列运算正确的是( )
| A. | -$\sqrt{-25}$=5 | B. | $\root{3}{1{0}^{6}}$=102 | C. | $\sqrt{4+\frac{9}{16}}$=2$\frac{3}{4}$ | D. | $\sqrt{0.25}$=±0.5 |
17.下列式子正确的是( )
| A. | $\sqrt{8}$=±2$\sqrt{2}$ | B. | $\root{3}{-8}$=-2 | C. | $\root{3}{-8}$=-2$\sqrt{2}$ | D. | $\sqrt{-8}$=-2$\sqrt{2}$ |
4.(-0.5)-2等于( )
| A. | 1 | B. | 4 | C. | -4 | D. | 0.25 |
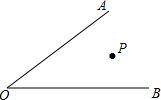 根据下列语句画图:如图,∠AOB内有一点P:
根据下列语句画图:如图,∠AOB内有一点P:
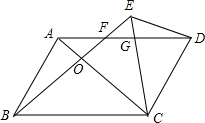 如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)
如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)