题目内容
3. 如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.
如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.
分析 AM⊥BC,DN⊥BC垂足分别为M、N,由AM=$\frac{1}{2}$BC,推出DN=$\frac{1}{2}$BD,推出∠DBN=30°,由此即可解决问题.
解答 解:如图作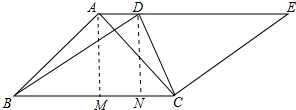 AM⊥BC,DN⊥BC垂足分别为M、N.
AM⊥BC,DN⊥BC垂足分别为M、N.
∵AB=AC,AB⊥AC,
∴∠BAC=90°,BM=CM,
∴AM=$\frac{1}{2}$BC,∠ABC=∠ACB=45°,
∵AD∥BC,AM∥DN,
∴四边形AMND是平行四边形,
∵∠AMN=90°,
∴四边形AMND是矩形,
∴AM=DN=$\frac{1}{2}$BC,
∵四边形BCED是菱形,
∴BD=BC,
∴DN=$\frac{1}{2}$BD,∵∠DNB=90°,
∴∠DBN=30°,
∴∠BCD=∠BDC=75°,
∴∠ACD=∠ACD-∠BCA=75°-45°=30°.
点评 本题考查菱形的性质、等腰直角三角形的性质、矩形的判定和性质等知识,解题的关键是30°的证明,在直角三角形中如果斜边是直角边的2倍,那么直角边所对的角是30°,属于中考常考题型.

练习册系列答案
相关题目
13.下列等式:①2ab+3ab=5a2b2;②(-5a3)2=25a6;③$\sqrt{x+y}$=$\sqrt{x}$+$\sqrt{y}$.其中正确的等式有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.若关于x的不等式组$\left\{\begin{array}{l}{x-m<0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个,则关于x的一元二次方程8x2-8x+m=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有一个实数根 |
8.如图是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm).将它们拼成如图的新几何体,则该新几何体的体积为( ) cm3. 

| A. | 48π | B. | 50π | C. | 58π | D. | 60π |
12.若A和B都是3次多项式,则A+B一定是( )
| A. | 6次多项式 | B. | 3次多项式 | ||
| C. | 次数不高于3次的多项式 | D. | 次数不低于3次的多项式 |
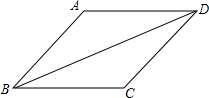 如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.
如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.