题目内容
11.已知关于x的方程(x-1)(x2-3x+m)=0,m为实数.(1)当m=4时,求方程的根;
(2)若方程的三个实根中恰好有两个实根相等,求m的值;
(3)若方程的三个实根恰好能成为一个三角形的三边长,求m的取值范围.
分析 (1)把m=4代入方程,得出(x-1)(x2-3x+4)=0,那么x-1=0或x2-3x+4=0,分别求解即可;
(2)由于x-1=0时x1=1,设方程x2-3x+m=0的两根为x2,x3,分x2=1,与x2=x3两种情况进行讨论;
(3)设方程x2-3x+m=0的两根为x2,x3,由根与系数的关系得出x2+x3=3,x2•x3=m.根据方程的三个实根恰好能成为一个三角形的三边长,得出$\left\{\begin{array}{l}m>0\\△=9-4m≥0\\|{x_2}-{x_3}|<1\end{array}\right.$,求解即可.
解答 解:(1)m=4时方程为(x-1)(x2-3x+4)=0,
得x-1=0或x2-3x+4=0,
由x-1=0得x=1,
由x2-3x+4=0得△=9-16=-7<0,该方程无实数解,
故方程的实根为x=1;
(2)由x-1=0得x1=1.
由x2-3x+m=0,得△=9-4m≥0,设方程两根为x2,x3,
若x2=1,则1-3+m=0,得m=2,方程为x2-3x+2=0,解得得x2=1,x3=2符合题意;
若x2=x3时,△=9-4m=0,得$m=\frac{9}{4}$,方程为${x^2}-3x+\frac{9}{4}=0$,得${x_2}={x_3}=\frac{3}{2}$,符合题意.
综上知m=2或$m=\frac{9}{4}$;
(3)方程的三个实根满足x1=1,
由x2-3x+m=0,得△=9-4m≥0,设方程两根为x2,x3,
则x2+x3=3,x2•x3=m,
方程的三个实根恰好能成为一个三角形的三边长,
则$\left\{\begin{array}{l}m>0\\△=9-4m≥0\\|{x_2}-{x_3}|<1\end{array}\right.$,
由$|{x_2}-{x_3}|=\sqrt{{{({{x_2}+{x_2}})}^2}-4{x_2}{x_3}}=\sqrt{9-4m}<1$,
得m>2,
解得$2<m≤\frac{9}{4}$.
点评 本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

 阅读快车系列答案
阅读快车系列答案| A. | 8.1×105平方米 | B. | 8.1×106平方米 | C. | 3.6×105平方米 | D. | 3.6×106平方米 |
| A. | 36.32×108 | B. | 3.632×108 | C. | 3.632×109 | D. | 0.3632×1010 |
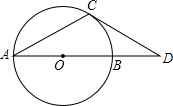 已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.
已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长. 如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.
如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.