题目内容
14.若关于x的不等式组$\left\{\begin{array}{l}{x-m<0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个,则关于x的一元二次方程8x2-8x+m=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有一个实数根 |
分析 首先解不等式组,利用m表示出不等式组的解集,然后根据不等式组有4个整数解即可求得m的范围,然后根据根的判别式即可得到结论.
解答 解:$\left\{\begin{array}{l}{x-m<0}\\{7-2x≤1}\end{array}\right.$,
由①得x<m,
由②得x≥3.
则不等式组的解集是3≤x<m.
∵不等式组有4个整数解,
∴不等式组的整数解是3,4,5,6.
∴6<m≤7,
∵△=64-32m<0,
∴方程没有实数根,
故选C.
点评 本题考查了根的判别式,不等式组的解法及整数解.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

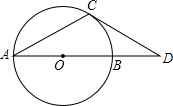 已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长.
已知,如图AB是⊙O的直径且AB=10,AC是弦,∠A=30°,过C作⊙O的切线交AB延长线于点D,求BD的长. 如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.
如图,四边形ABCD为梯形,BCED为菱形,AB⊥AC,AB=AC.求∠ACD.