题目内容
14.先化简,再求值:$\frac{{a}^{2}-3a}{{a}^{2}+a}$÷$\frac{a-3}{{a}^{2}-1}$•$\frac{a+1}{a-1}$,其中a=2016.分析 先算除法,再算乘法,把分式化为最简形式,最后把a=2016代入进行计算即可.
解答 解:原式=$\frac{a(a-3)}{a(a+1)}$•$\frac{(a+1)(a-1)}{a-3}$•$\frac{a+1}{a-1}$
=(a-1)•$\frac{a+1}{a-1}$
=a+1,
当a=2016时,原式=2017.
点评 本题考查的是分式的化简求值,在解答此类问题时要注意把分式化为最简形式,再代入求值.

练习册系列答案
相关题目
5.一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
| A. | 13cm | B. | 14cm | C. | 13cm或14cm | D. | 以上都不对 |
9.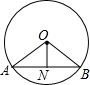 如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
 如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
19.-$\frac{1}{6}$的相反数是( )
| A. | $\frac{1}{6}$ | B. | -6 | C. | 6 | D. | -$\frac{1}{6}$ |
3. 如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠BCD=( )
如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠BCD=( )
 如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠BCD=( )
如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠BCD=( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
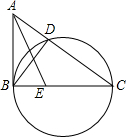 如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB. 如图所示,矩形PDOC的边OC在x轴上,OD在y轴上,点P在第一象限,双曲线y=$\frac{k}{x}$经过点P,双曲线y=$\frac{2}{x}$交PD于点B,交PC于点A,四边形PBOA的面积为6.
如图所示,矩形PDOC的边OC在x轴上,OD在y轴上,点P在第一象限,双曲线y=$\frac{k}{x}$经过点P,双曲线y=$\frac{2}{x}$交PD于点B,交PC于点A,四边形PBOA的面积为6.