题目内容
4.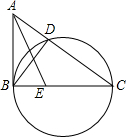 如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4,tan∠AEB=$\frac{5}{3}$,AB:BC=2:3,求圆的直径.
分析 (1)欲证明AB是圆的切线,只要证明∠ABC=90°即可.
(2)在RT△AEB中,根据tan∠AEB=$\frac{5}{3}$,求出BC,在RT△ABC中,根据$\frac{AB}{BC}$=$\frac{2}{3}$求出AB即可.
解答 (1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ACB+∠DBC=90°,
∵∠ABD=∠ACB,
∴∠ABD+∠DBC=90°
∴∠ABC=90°
∴AB⊥BC,
∴AB是圆的切线.
(2)解:在RT△AEB中,tan∠AEB=$\frac{5}{3}$,
∴$\frac{AB}{BE}$=$\frac{5}{3}$,即AB=$\frac{5}{3}$BE=$\frac{20}{3}$,
在RT△ABC中,$\frac{AB}{BC}$=$\frac{2}{3}$,
∴BC=$\frac{3}{2}$AB=10,
∴圆的直径为10.
点评 本题考查切线的判定、三角函数等知识,解题的关键是记住经过半径的外端垂直于半径的直线是圆的切线,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.实数a,b互为相反数,则下列结论正确的是( )
| A. | a+b=0 | B. | ab=1 | C. | a÷b=-l | D. | a>0,b<0 |
15. 如图是一个正方体的平面展开图,那么这个正方体“美”字的对面所标的字是( )
如图是一个正方体的平面展开图,那么这个正方体“美”字的对面所标的字是( )
 如图是一个正方体的平面展开图,那么这个正方体“美”字的对面所标的字是( )
如图是一个正方体的平面展开图,那么这个正方体“美”字的对面所标的字是( )| A. | 让 | B. | 更 | C. | 活 | D. | 生 |
12.说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 含30°的直角三角形 | D. | 顶角为45°的等腰三角形 |
9.已知a≠0,下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | (a2)3=a5 | C. | a2•a4=a8 | D. | a4÷a3=a |
16. 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )| A. | $\frac{15\sqrt{3}}{4}$-$\frac{3}{2}π$ | B. | $\frac{15\sqrt{3}}{2}$-$\frac{3}{2}π$ | C. | $\frac{7\sqrt{3}}{4}$-$\frac{π}{6}$ | D. | $\frac{7\sqrt{3}}{2}$-$\frac{π}{6}$ |
13.关于?ABCD的叙述,正确的是( )
| A. | 若AB⊥BC,则?ABCD是菱形 | B. | 若AC⊥BD,则?ABCD是正方形 | ||
| C. | 若AC=BD,则?ABCD是矩形 | D. | 若AB=AD,则?ABCD是正方形 |
