题目内容
14.解方程组:$\left\{\begin{array}{l}{3x-4y+11=0}\\{3y-4x+53=0}\end{array}\right.$.分析 根据加减消元法,可得方程组的解.
解答 解:$\left\{\begin{array}{l}{3x-4y+11=0①}\\{3y-4x+53=0②}\end{array}\right.$,
①×4+②×3,得
-7y+203=0.解得y=27,
把y=27代入②,得
81-4x+53=0.
解得x=33.5
原方程组的解为$\left\{\begin{array}{l}{x=33.5}\\{y=27}\end{array}\right.$.
点评 本题考查了解二元一次方程组,利用加减校园法界方程组的关键是:将相同项的系数化为相等的数或互为相反数是解题关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
20.甲厂每天早上派出20辆车,去乙厂装载A,B,C三种原料共36吨运回甲厂,每辆车装载原料时必须满载.每种原料不能少于一车,且A,B,C三种原料不能混装,每辆汽车的装载情况及运费如下表所示:
请解答下列问题
(1)甲厂有哪几种运进原料的方案;
(2)甲厂按哪种方案运进原料所花费的运费最低,最低运费是多少;
(3)在(1)的条件下,某天早上,甲厂根据当天的生产计划及当时原料仓库所剩余的原料情况,决定当天听出的车辆所运回的C种原料不得少于6吨,请直接写出当天甲厂运进原料的最低费用是多少.
| 原料型号 | A | B | C |
| 每辆车的装载重量(吨) | 2 | 1 | 1.5 |
| 每辆车的运输费用(元 | 50 | 70 | 80 |
(1)甲厂有哪几种运进原料的方案;
(2)甲厂按哪种方案运进原料所花费的运费最低,最低运费是多少;
(3)在(1)的条件下,某天早上,甲厂根据当天的生产计划及当时原料仓库所剩余的原料情况,决定当天听出的车辆所运回的C种原料不得少于6吨,请直接写出当天甲厂运进原料的最低费用是多少.
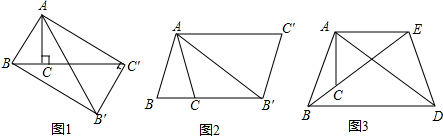
 如图,某高铁工程需要确定隧道CD的长度,测量人员在离地面1000米高的A处的飞机上,测得C点的俯角为45°,然后飞机沿与水平线成30°角的方向飞行到离地面2000米高的B点,测得D点的俯角为60°,求隧道CD的长(结果精确到0.1米,$\sqrt{3}$≈1.732).
如图,某高铁工程需要确定隧道CD的长度,测量人员在离地面1000米高的A处的飞机上,测得C点的俯角为45°,然后飞机沿与水平线成30°角的方向飞行到离地面2000米高的B点,测得D点的俯角为60°,求隧道CD的长(结果精确到0.1米,$\sqrt{3}$≈1.732).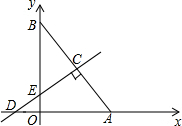 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上,且A(6,0),cos∠BAO=$\frac{3}{5}$,线段AB的垂直平分线CD交AB于点C,交y轴于点E,交x轴于点D.
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上,且A(6,0),cos∠BAO=$\frac{3}{5}$,线段AB的垂直平分线CD交AB于点C,交y轴于点E,交x轴于点D.