题目内容
20.甲厂每天早上派出20辆车,去乙厂装载A,B,C三种原料共36吨运回甲厂,每辆车装载原料时必须满载.每种原料不能少于一车,且A,B,C三种原料不能混装,每辆汽车的装载情况及运费如下表所示:| 原料型号 | A | B | C |
| 每辆车的装载重量(吨) | 2 | 1 | 1.5 |
| 每辆车的运输费用(元 | 50 | 70 | 80 |
(1)甲厂有哪几种运进原料的方案;
(2)甲厂按哪种方案运进原料所花费的运费最低,最低运费是多少;
(3)在(1)的条件下,某天早上,甲厂根据当天的生产计划及当时原料仓库所剩余的原料情况,决定当天听出的车辆所运回的C种原料不得少于6吨,请直接写出当天甲厂运进原料的最低费用是多少.
分析 (1)根据题意表示出运载三种原料的车辆数,进而利用已知分析得出符合题意的答案;
(2)结合(1)中所求得出最低费用;
(3)结合(1)中所求得出最低费用,以及所运回的C种原料不得少于6吨得出答案.
解答 解:(1)设装载A原料的车辆为x辆,装载B原料的车辆为y辆,则装载C原料的车辆为(20-x-y)辆,根据题意可得:
2x+y+1.5(20-x-y)=36,
整理得:x-y=12,
∵每种原料不能少于一车,
∴当y=1,则x=13,20-x-y=6,即装载A原料的车辆为13辆,装载B原料的车辆为1辆,则装载C原料的车辆为6辆;
当y=2,则x=14,20-x-y=4,即装载A原料的车辆为14辆,装载B原料的车辆为2辆,则装载C原料的车辆为4辆;
当y=3,则x=15,20-x-y=2,即装载A原料的车辆为15辆,装载B原料的车辆为3辆,则装载C原料的车辆为2辆;
故一共有3种方案;
(2)由图表中数据可得:只有A原料的运费最低,故甲厂按第3种方案运进原料所花费的运费最低,
最低运费是:15×50+3×70+2×80=1120(元);
(3)∵当天运出的车辆所运回的C种原料不得少于6吨,
∴装载A原料的车辆为14辆,装载B原料的车辆为2辆,则装载C原料的车辆为4辆此时运费最低,
总运费为:14×50+2×70+4×80=1160(元).
点评 此题主要考查了二元一次方程的应用,根据题意得出正确等量关系进而得出符合题意的答案是解题关键.

练习册系列答案
相关题目
13.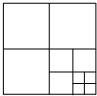 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
(1)将下表填写完整;
(2)an=3n+1(用含n的代数式表示);
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.
 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.(1)将下表填写完整;
| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.