题目内容
20. 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.| A. | 60° | B. | 45° | C. | 30° | D. | 36° |
分析 连接OB,OC,根据四边形ABCD是正方形可知∠BOC=90°,再由圆周角定理即可得出结论.
解答 解: 连接OB,OC,
连接OB,OC,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴∠BPC=$\frac{1}{2}$∠BOC=45°.
故选B.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
12.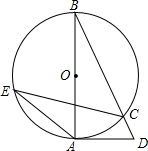 如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
 如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 74° |
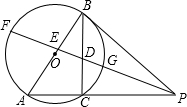 已知:如图AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,PF分别交AB、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.
已知:如图AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,PF分别交AB、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.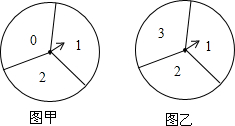 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$.
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$.