题目内容
15.请在下列两个小题中,任选其一完成即可(1)解方程:$\frac{1}{x-3}$+2=$\frac{4-x}{3-x}$;
(2)已知二次函数y=-2x2+8x.用配方法把该函数化为y=a(x-h)2+k(其中a、h、k都是常数且a≠0)的形式,并指出函数图象的对称轴和顶点坐标.
分析 (1)根据解分式方程的步骤:去分母、去括号、移项、合并同类项、系数化为1解出方程,验根得到答案;
(2)把一般式用配方法化为顶点式,根据二次函数的性质找出对称轴和顶点坐标.
解答 解:(1)去分母:1+2(x-3)=x-4
去括号:1+2x-6=x-4
移项:2x-x=-4-1+6
合并:x=1
检验:把x=1代入x-3得-2≠0,所以x=1是原分式方程的解.
(2)y=-2x2+8x
=-2(x2-4x)
=-2(x2-4x+4-4)
=-2(x2-4x+4)+8
=-2(x-2)2+8
所以对称轴为:x=2,
顶点坐标:(2,4).
点评 本题考查的是二次函数的三种形式,掌握配方法是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
5.两个边长分别为1,2,$\sqrt{5}$的三角形,拼成一个四边形,则能拼成几种不同的四边形.( )
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
20. 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.| A. | 60° | B. | 45° | C. | 30° | D. | 36° |
7. 如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
 如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )| A. | 120° | B. | 135° | C. | 240° | D. | 315° |
5.-3,0,-1,2四个数中,绝对值最大的数是( )
| A. | -3 | B. | 0 | C. | 2 | D. | -1 |
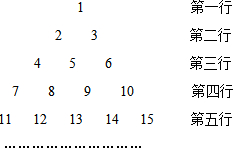 如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2π}{3}$,则图中阴影部分的面积为$\frac{{3\sqrt{3}}}{2}-\frac{2}{3}π$.
如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2π}{3}$,则图中阴影部分的面积为$\frac{{3\sqrt{3}}}{2}-\frac{2}{3}π$.