题目内容
12．
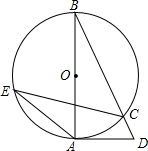如图，AB为⊙O的直径，点E、C都在圆上，连接AE，CE，BC，过点A作⊙O的切线交BC的延长线于点D，若∠AEC=25°，则∠D的度数为（ ）| A． | 75° | B． | 65° | C． | 55° | D． | 74° |
分析 根据圆周角定理得出∠B=∠AEC=25°，根据切线的性质求出∠BAD，进一步根据三角形的内角和求出答案即可即可．
解答 解：∵过点A作⊙O的切线交BC的延长线于点D，
∴∠BAD=90°，
∵∠AEC=25°，
∴∠B=∠AEC=25°，
∴∠D=180°-90°-25°=65°．
故选：B．
点评 本题考查了切线的性质，圆周角定理的应用，结合图形灵活运用这些性质进行推理得出答案即可．
练习册系列答案
相关题目
20．
如图，正方形ABCD是⊙O的内接正方形，点P是劣弧AB上不同于点B的任意一点，则∠BPC为（ ）度．
如图，正方形ABCD是⊙O的内接正方形，点P是劣弧AB上不同于点B的任意一点，则∠BPC为（ ）度．| A． | 60° | B． | 45° | C． | 30° | D． | 36° |
7．
如图，已知△ABC为等边三角形，若沿图中虚线剪去∠B，则∠1+∠2等于（ ）
如图，已知△ABC为等边三角形，若沿图中虚线剪去∠B，则∠1+∠2等于（ ）| A． | 120° | B． | 135° | C． | 240° | D． | 315° |
如图，以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点，交直角边AC于点E．B、E是半圆弧的三等分点，弧BE的长为$\frac{2π}{3}$，则图中阴影部分的面积为$\frac{{3\sqrt{3}}}{2}-\frac{2}{3}π$．
1．为了参加市中学生篮球运动会，一支校篮球队准备购买10双运动鞋，各种尺码的统计如下表所示，则这10双运动鞋尺码的众数和中位数分别为（ ）
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A． | 25.5，26 | B． | 26，25.5 | C． | 26，26 | D． | 25.5，25.5 |