题目内容
11.(1)计算:($\sqrt{2015}$-1)0+$\sqrt{18}$sin45°-2-2;(2)解不等式组:$\left\{\begin{array}{l}{x-1>0}\\{\frac{x}{2}≤\frac{x+1}{3}}\end{array}\right.$
(3)解方程:x2-4x+1=0.
分析 (1)原式第一项利用零指数幂法则计算,第二项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出不等式组的解集;
(3)找出a,b,c的值,代入求根公式即可求出解.
解答 解:(1)原式=1+3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-$\frac{1}{4}$=3$\frac{3}{4}$;
(2)$\left\{\begin{array}{l}{x-1>0①}\\{\frac{x}{2}≤\frac{x+1}{3}②}\end{array}\right.$,
由①得:x>1;
由②得:x≤2,
则不等式组的解集为1<x≤2;
(3)这里a=1,b=-4,c=1,
∵△=16-4=12,
∴x=$\frac{4±2\sqrt{3}}{2}$=2±$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
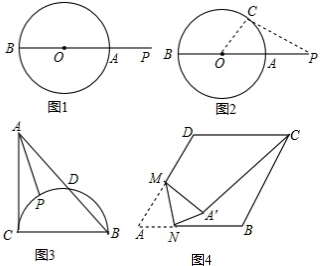
20. 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧AB上不同于点B的任意一点,则∠BPC为( )度.| A. | 60° | B. | 45° | C. | 30° | D. | 36° |
1.为了参加市中学生篮球运动会,一支校篮球队准备购买10双运动鞋,各种尺码的统计如下表所示,则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5,26 | B. | 26,25.5 | C. | 26,26 | D. | 25.5,25.5 |
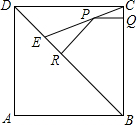 如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=$\sqrt{2}$-1;(2)PQ+PR=$\frac{\sqrt{2}}{2}$.
如图,E是边长为1的正方形ABCD的对角线BD上的一点,且BE=BA,P是CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R.则:(1)DE=$\sqrt{2}$-1;(2)PQ+PR=$\frac{\sqrt{2}}{2}$.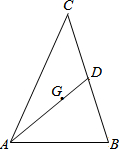 如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.
如图,G是△ABC的重心,连接AG并延长交BC于D,已知AG=2$\sqrt{3}$+2,∠BAD=45°,∠B=75°,则BC=12.