题目内容
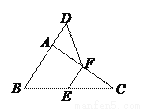
如图,在△ABC中,∠BAC=90º,延长BA到点D,使AD=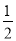 AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
 见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E...
见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E...
练习册系列答案
相关题目
若关于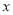 的方程
的方程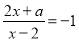 的解为正数,则
的解为正数,则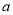 的取值范围是_____.
的取值范围是_____.
 且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且.
且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且. 化简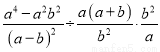 的结果是( )
的结果是( )
A. 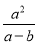 B.
B. 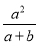 C.
C. 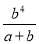 D.
D. 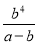
 D
【解析】试题解析:原式
故选D.
D
【解析】试题解析:原式
故选D. 填空:  =1÷(____),
=1÷(____),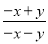 =﹣(____) ÷(x+y).
=﹣(____) ÷(x+y).
 x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y).
x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y). 使分式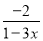 的值为正的条件是( )
的值为正的条件是( )
A. 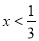 B.
B. 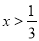 C. x<0 D. x>0
C. x<0 D. x>0
 B
【解析】由题意得
1-3x<0,
解之得
.
故选B.
B
【解析】由题意得
1-3x<0,
解之得
.
故选B. 如图,在四边形ABCD中,P是BC边上一点,∠A=∠B=90º,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
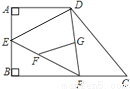
 【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.
【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=. 如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
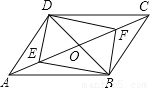
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B. 分式方程 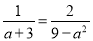 的解是_______.
的解是_______.
 1
【解析】去分母得:3-a=2,解得:a=1,检验:当a=1时,9-a²≠0,所以原方程的解是:a=1.故答案为:a=1.
1
【解析】去分母得:3-a=2,解得:a=1,检验:当a=1时,9-a²≠0,所以原方程的解是:a=1.故答案为:a=1. 化简 的结果是( )
的结果是( )
A.m+n B.n﹣m C.m﹣n D.﹣m﹣n
 A.
【解析】
试题分析:====m+n.故选A.
A.
【解析】
试题分析:====m+n.故选A. 
