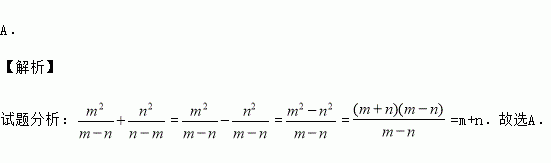题目内容
化简
的结果是（ ）
A．m+n B．n﹣m C．m﹣n D．﹣m﹣n
A．
【解析】
试题分析：====m+n．故选A．
练习册系列答案
高中必刷题系列答案
相关题目
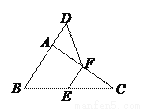
如图，在△ABC中，∠BAC=90º，延长BA到点D，使AD=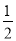
AB，E，F分别是边BC，AC的中点，试猜想DF与EC的数量关系，并证明你的猜想.
见解析
【解析】试题分析：由直角三角形的性质和三角形中位线定理得出AE=BC=EC，EF∥AB，EF=
AB，得出AD∥EF，AD=EF，证出四边形AEFD是平行四边形，得出AE=DF，即可得出结论．
【解析】
DF=EC；理由如下：
连接AE,如图所示：
∵∠BAC=90°，E，F分别是边BC，AC的中点，
∴AE=BC=EC,E... 如果关于x的方程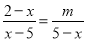
无解，则m等于（ ）
A. 3 B. 4 C. -3 D. 5
A
【解析】去分母，得2－x＝－m，所以x＝2＋m.
若分式方程无解，则x＝2＋m是分式方程的增根，即2＋m＝5，
所以m＝3.
故答案为：3. 小明用电脑录入汉字文稿的速度是他手抄汉字文稿速度的4倍，若小明手抄汉字文稿的速度为m个字/小时．那么他用电脑录入4000字文稿比手抄少用多少小时？
(小时)．
【解析】试题分析：根据手抄录入时间-电脑录入时间=时间差列出代数式运算即可.
试题解析：根据题意，可得：
他用电脑录入4000字文稿比手抄少用小时.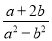 
－
＝_____.
【解析】试题解析：原式
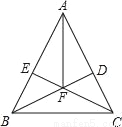
故答案为： 如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴... 等腰三角形周长为36cm，两边长之比为4：1，则底边长为（ ）
A. 16cm B. 4cm C. 20cm D. 16cm或4cm
B
【解析】因为两边长之比为4：1，所以设较短一边为x，则另一边为4x；
(1)假设x为底边，4x为腰；则8x+x=36，x=4，即底边为4；
(2)假设x为腰，4x为底边，则2x+4x=36，x=6，4x=24；
∵6+6＜24，∴该假设不成立．
所以等腰三角形的底边为4cm．
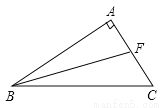
故选B. 如图，AB⊥AC，BF是∠ABC的平分线，若∠BFC=110°，求∠C的度数.
∠C=50°
【解析】试题分析：因为∠BFC=110°，根据三角形的外角等于不相邻的两个内角之和，可以得到∠ABF+∠A=110° ，所以∠ABF=110°－90°=20°，因为BF是∠ABC的角平分线，所以可以得到∠ABC=2∠ABF=40°，即在△ABC中∠C=180°－90°－40°=50°.
试题解析：
∵∠BFC=110°，
∴∠ABF=110°－90°=20°，... （5-x2）2等于_______；
25-10x2+x4
【解析】根据完全平方公式可得：（5-x2）2=25-10x2+x4.