题目内容
化简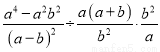 的结果是( )
的结果是( )
A. 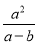 B.
B. 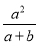 C.
C. 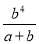 D.
D. 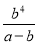
 D
【解析】试题解析:原式
故选D.
D
【解析】试题解析:原式
故选D.
练习册系列答案
相关题目
在四边形ABCD中,如果∠A:∠B:∠C:∠D=1:2:3:4,则∠D=______
 144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°.
144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°. 若分式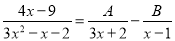 (A、B为常数),则A、B 的值为 ( )
(A、B为常数),则A、B 的值为 ( )
A. 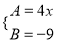 B.
B. 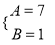 C.
C. 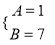 D.
D. 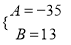
 B
【解析】= ,则 ,故选B.
B
【解析】= ,则 ,故选B. 先化简,再求值.
(1) 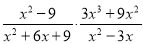 ,其中x=-
,其中x=-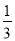 .
.
(2)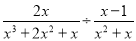 ,其中x=-2.
,其中x=-2.
(3)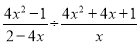 ,其中x=-
,其中x=-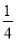 .
.
(4)若1<x<2,化简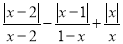 .
.
 ⑴-1,⑵ ,⑶,⑷1.
【解析】试题分析:(1)原式约分得到最简结果,将x的值代入计算即可求出值;
(2)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,将x的值代入计算即可求出值;
(3)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,将x的值代入计算即可求出值.
(4)根据绝对值的化简原则进行化简,进行运算即可....
⑴-1,⑵ ,⑶,⑷1.
【解析】试题分析:(1)原式约分得到最简结果,将x的值代入计算即可求出值;
(2)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,将x的值代入计算即可求出值;
(3)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,将x的值代入计算即可求出值.
(4)根据绝对值的化简原则进行化简,进行运算即可.... 计算 =_________.
=_________.
 【解析】试题解析:原式=
故答案为:
【解析】试题解析:原式=
故答案为: 计算﹣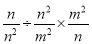 的结果为( )
的结果为( )
A. ﹣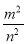 B. ﹣
B. ﹣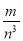 C. ﹣
C. ﹣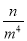 D. ﹣n
D. ﹣n
 A
【解析】【解析】
原式= .故选A.
A
【解析】【解析】
原式= .故选A. 当y=x+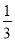 时,
时,  的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
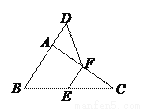
∴原式==-3. 如图,在△ABC中,∠BAC=90º,延长BA到点D,使AD=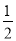 AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
 见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E...
见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E... 如果关于x的方程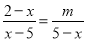 无解,则m等于( )
无解,则m等于( )
A. 3 B. 4 C. -3 D. 5
 A
【解析】去分母,得2-x=-m,所以x=2+m.
若分式方程无解,则x=2+m是分式方程的增根,即2+m=5,
所以m=3.
故答案为:3.
A
【解析】去分母,得2-x=-m,所以x=2+m.
若分式方程无解,则x=2+m是分式方程的增根,即2+m=5,
所以m=3.
故答案为:3.