题目内容
如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
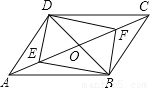
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若分式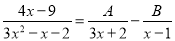 (A、B为常数),则A、B 的值为 ( )
(A、B为常数),则A、B 的值为 ( )
A. 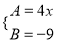 B.
B. 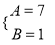 C.
C. 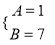 D.
D. 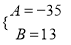
 B
【解析】= ,则 ,故选B.
B
【解析】= ,则 ,故选B. 当y=x+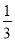 时,
时,  的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
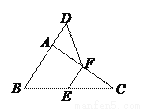
∴原式==-3. 如图,在△ABC中,∠BAC=90º,延长BA到点D,使AD=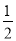 AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
 见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E...
见解析
【解析】试题分析:由直角三角形的性质和三角形中位线定理得出AE=BC=EC,EF∥AB,EF=
AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解析】
DF=EC;理由如下:
连接AE,如图所示:
∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=BC=EC,E... 平行四边形两邻边长分别为20和16,若两条较长边之间的距离为6,则两条较短边之间的距离为_______.
 7.5
【解析】由题意得
20×6÷16=7.5cm.
7.5
【解析】由题意得
20×6÷16=7.5cm. 如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
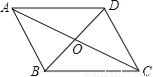
A. 18 B. 28 C. 36 D. 46
 C
【解析】试题分析:由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
【解析】
∵四边形ABCD是平行四边形,
∴AB=CD=5,
∵△OCD的周长为23,
∴OD+OC=23﹣5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=...
C
【解析】试题分析:由平行四边形的性质和已知条件计算即可,解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体.
【解析】
∵四边形ABCD是平行四边形,
∴AB=CD=5,
∵△OCD的周长为23,
∴OD+OC=23﹣5=18,
∵BD=2DO,AC=2OC,
∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=... 解分式方程: 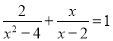
 .
【解析】试题分析:首先进行去分母,将分式方程转化为整式方程,然后求出方程的解,最后需要对方程的解进行检验,看是否能使原分式的分母为零.
试题解析:去分母得:2+x(x+2)=x2-4, 解得:x=-3,
检验:当x=-3时,(x+2)(x-2)≠0,
故x=-3是原方程的根.
.
【解析】试题分析:首先进行去分母,将分式方程转化为整式方程,然后求出方程的解,最后需要对方程的解进行检验,看是否能使原分式的分母为零.
试题解析:去分母得:2+x(x+2)=x2-4, 解得:x=-3,
检验:当x=-3时,(x+2)(x-2)≠0,
故x=-3是原方程的根. 如果关于x的方程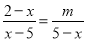 无解,则m等于( )
无解,则m等于( )
A. 3 B. 4 C. -3 D. 5
 A
【解析】去分母,得2-x=-m,所以x=2+m.
若分式方程无解,则x=2+m是分式方程的增根,即2+m=5,
所以m=3.
故答案为:3.
A
【解析】去分母,得2-x=-m,所以x=2+m.
若分式方程无解,则x=2+m是分式方程的增根,即2+m=5,
所以m=3.
故答案为:3. 等腰三角形周长为36cm,两边长之比为4:1,则底边长为( )
A. 16cm B. 4cm C. 20cm D. 16cm或4cm
 B
【解析】因为两边长之比为4:1,所以设较短一边为x,则另一边为4x;
(1)假设x为底边,4x为腰;则8x+x=36,x=4,即底边为4;
(2)假设x为腰,4x为底边,则2x+4x=36,x=6,4x=24;
∵6+6<24,∴该假设不成立.
所以等腰三角形的底边为4cm.
故选B.
B
【解析】因为两边长之比为4:1,所以设较短一边为x,则另一边为4x;
(1)假设x为底边,4x为腰;则8x+x=36,x=4,即底边为4;
(2)假设x为腰,4x为底边,则2x+4x=36,x=6,4x=24;
∵6+6<24,∴该假设不成立.
所以等腰三角形的底边为4cm.
故选B. 
