题目内容
分式方程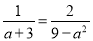 
的解是_______.
1
【解析】去分母得：3-a=2,解得：a=1,检验:当a=1时，9-a²≠0,所以原方程的解是：a=1.故答案为：a=1.
练习册系列答案
阅读快车系列答案
相关题目
先化简，再求值．
(1) 
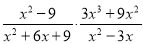，其中x＝-
．
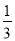（2）
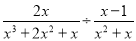，其中x=－2．
（3）
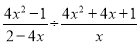，其中x=-
．
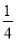（4）若1＜x＜2，化简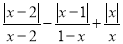
．
⑴－１，⑵ ，⑶，⑷1．
【解析】试题分析：（1）原式约分得到最简结果，将x的值代入计算即可求出值；
（2）原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到最简结果，将x的值代入计算即可求出值；
（3）原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到最简结果，将x的值代入计算即可求出值．
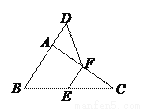
（4）根据绝对值的化简原则进行化简，进行运算即可.... 如图，在△ABC中，∠BAC=90º，延长BA到点D，使AD=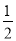
AB，E，F分别是边BC，AC的中点，试猜想DF与EC的数量关系，并证明你的猜想.
见解析
【解析】试题分析：由直角三角形的性质和三角形中位线定理得出AE=BC=EC，EF∥AB，EF=
AB，得出AD∥EF，AD=EF，证出四边形AEFD是平行四边形，得出AE=DF，即可得出结论．
【解析】
DF=EC；理由如下：
连接AE,如图所示：
∵∠BAC=90°，E，F分别是边BC，AC的中点，
∴AE=BC=EC,E... 如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）
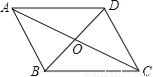
A. 18 B. 28 C. 36 D. 46
C
【解析】试题分析：由平行四边形的性质和已知条件计算即可，解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体．
【解析】
∵四边形ABCD是平行四边形，
∴AB=CD=5，
∵△OCD的周长为23，
∴OD+OC=23﹣5=18，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=... 解分式方程：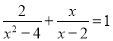 
.
【解析】试题分析：首先进行去分母，将分式方程转化为整式方程，然后求出方程的解，最后需要对方程的解进行检验，看是否能使原分式的分母为零.
试题解析：去分母得：2+x（x+2）=x2-4， 解得：x=-3，
检验：当x=-3时，（x+2）（x-2）≠0，
故x=-3是原方程的根． 若分式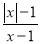
的值为0，则x的值等于___________
-1
【解析】试题分析：因为当时分式的值为零，解得且，所以x=1． 如果关于x的方程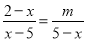
无解，则m等于（ ）
A. 3 B. 4 C. -3 D. 5
A
【解析】去分母，得2－x＝－m，所以x＝2＋m.
若分式方程无解，则x＝2＋m是分式方程的增根，即2＋m＝5，
所以m＝3.
故答案为：3. 小明用电脑录入汉字文稿的速度是他手抄汉字文稿速度的4倍，若小明手抄汉字文稿的速度为m个字/小时．那么他用电脑录入4000字文稿比手抄少用多少小时？
(小时)．
【解析】试题分析：根据手抄录入时间-电脑录入时间=时间差列出代数式运算即可.
试题解析：根据题意，可得：
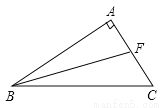
他用电脑录入4000字文稿比手抄少用小时. 如图，AB⊥AC，BF是∠ABC的平分线，若∠BFC=110°，求∠C的度数.
∠C=50°
【解析】试题分析：因为∠BFC=110°，根据三角形的外角等于不相邻的两个内角之和，可以得到∠ABF+∠A=110° ，所以∠ABF=110°－90°=20°，因为BF是∠ABC的角平分线，所以可以得到∠ABC=2∠ABF=40°，即在△ABC中∠C=180°－90°－40°=50°.
试题解析：
∵∠BFC=110°，
∴∠ABF=110°－90°=20°，...