题目内容
9.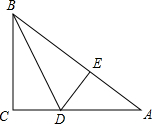 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.(1)求CD的长;
(2)求tan∠DBC的值.
分析 (1)根据正弦的概念和勾股定理求出DE的值,根据角平分线的性质求出CD的长;
(2)根据相似三角形的判定和性质求出AB、BE、BC的长,根据正切的概念计算得到答案.
解答 解:(1)∵sinA=$\frac{3}{5}$,
∴$\frac{DE}{AD}$=$\frac{3}{5}$,
设DE=3x,则DA=5x,
由勾股定理得,(5x)2-(3x)2=82,
解得x=2,
∴DE=3x=6,DA=5x=10,
∵BD平分∠ABC,DE⊥AB,∠C=90°,
∴CD=DE=6;
(2)∵DE⊥AB,∠C=90°,
∴△AED∽△ACB,
∴$\frac{AD}{AB}$$\frac{AE}{AC}$,即$\frac{10}{AB}$=$\frac{8}{16}$,
解得AB=20,
则BE=AB-AE=12,
∴BC=12,
则tan∠DBC=$\frac{CD}{BC}$=$\frac{1}{2}$.
点评 本题考查的是角平分线的性质、相似三角形的判定和性质、锐角三角函数的概念,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
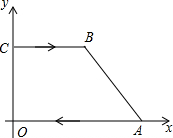 四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒
四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒 如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,求BE的长.
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,求BE的长. 如图,在△ABC中,PA,PB分别平分∠BAC和∠ABC,PH⊥AB,垂足为H,已知∠C=90°,BC=3,AC=4,求PH的长.
如图,在△ABC中,PA,PB分别平分∠BAC和∠ABC,PH⊥AB,垂足为H,已知∠C=90°,BC=3,AC=4,求PH的长. 如图,在等腰△ABC中,过点A作CB的高,交CB的延长线于点D,若AB=2,∠ABC=120°,求sinC-tanC的值.
如图,在等腰△ABC中,过点A作CB的高,交CB的延长线于点D,若AB=2,∠ABC=120°,求sinC-tanC的值. 如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长.
如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长. 如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.
如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.