题目内容
已知在平面直角坐标系中,四边形OABC是矩形,点A、C的坐标分别为A(3,0)、C(0,4),点D的坐标为D(-5,0),点P是直线AC上的一动点,直线DP与y轴交于点M.问:
(1)当点P运动到何位置时,直线DP平分矩形OABC的面积?请在图中画出P的位置,并且直接写出此时P点的坐标;
(2)当点P沿直线AC移动时,是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、半径长为R(R>0)画圆,所得到的圆称为动圆P.若设动圆P的直径长为AC,过点D作动圆P的两条切线,切点分别为点E、F.请探求四边形DEPF的面积是否存在最小值?若存在,请求出此时DP的长度;若不存在,请说明理由.
注:第(3)问请用备用图解答.
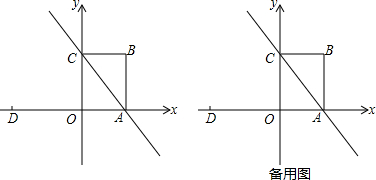
(1)当点P运动到何位置时,直线DP平分矩形OABC的面积?请在图中画出P的位置,并且直接写出此时P点的坐标;
(2)当点P沿直线AC移动时,是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、半径长为R(R>0)画圆,所得到的圆称为动圆P.若设动圆P的直径长为AC,过点D作动圆P的两条切线,切点分别为点E、F.请探求四边形DEPF的面积是否存在最小值?若存在,请求出此时DP的长度;若不存在,请说明理由.
注:第(3)问请用备用图解答.

考点:一次函数综合题
专题:
分析:(1)根据过对角线交点的直线平分矩形,可得P点坐标是AC的中点,根据中点的性质,可得P点坐标;
(2)根据相似三角形的性质,可得对应边的比成比例,根据比例的性质,可得答案;
(3)根据DF=DE最短,可得四边形DEPF面积最小,根据垂线段的长度最短,可得DP⊥AC,可得DP与AC的交点,可得P点坐标,根据两点间的距离,可得DP的长.
(2)根据相似三角形的性质,可得对应边的比成比例,根据比例的性质,可得答案;
(3)根据DF=DE最短,可得四边形DEPF面积最小,根据垂线段的长度最短,可得DP⊥AC,可得DP与AC的交点,可得P点坐标,根据两点间的距离,可得DP的长.
解答:解:(1)当点P运动到AC的中点时,直线DP平分矩形OABC的面积,P(
,2);
(2)△DOM∽△ABC时,
=
,
=
,OM=
,即M(0,
);
△DOM∽△CBA时,
=
,
=
,OM=
即M(0,
);
(3)如图:

当DP⊥AC时,四边形DEPF的面积存在最小值,
AC的解析式为y=-
x+4,
DP⊥AC时,kDP=
,
设DP的解析式为y=
x+b.
把D(-5,0)代入函数解析式y=
x+b,得
×(-5)+b=0.
解得b=
,
DP的解析式y=
x+
,
P点坐标是DP与AC的交点,得
,
解得
,
p(
,
).
DP=
=
=
=
| 3 |
| 2 |
(2)△DOM∽△ABC时,
| DO |
| AB |
| OM |
| BC |
| 5 |
| 4 |
| OM |
| 3 |
| 15 |
| 4 |
| 15 |
| 4 |
△DOM∽△CBA时,
| DO |
| CB |
| OM |
| BA |
| 5 |
| 3 |
| OM |
| 4 |
| 20 |
| 3 |
| 20 |
| 3 |
(3)如图:

当DP⊥AC时,四边形DEPF的面积存在最小值,
AC的解析式为y=-
| 4 |
| 3 |
DP⊥AC时,kDP=
| 3 |
| 4 |
设DP的解析式为y=
| 3 |
| 4 |
把D(-5,0)代入函数解析式y=
| 3 |
| 4 |
| 3 |
| 4 |
解得b=
| 15 |
| 4 |
DP的解析式y=
| 3 |
| 4 |
| 15 |
| 4 |
P点坐标是DP与AC的交点,得
|
解得
|
p(
| 3 |
| 25 |
| 384 |
| 100 |
DP=
(
|
|
| 640 |
| 100 |
| 32 |
| 5 |
点评:本题考查了一次函数综合题,利用了矩形的性质:过矩形对角线的点的直线平分矩形,相似三角形的性质,一直角边的长一定,斜边长越短另一直角边越短,面积越小,计算量大要认真计算.

练习册系列答案
相关题目
 求阴影部分面积.
求阴影部分面积. 甲乙两人分别从相距90千米的A、B两地出发相向而行,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,乙到达A地停止.如图是他们离各自出发地的距离y(千米)与甲行驶时间x(小时)之间的函数关系图象,请结合图象信息,解答下列问题:
甲乙两人分别从相距90千米的A、B两地出发相向而行,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,乙到达A地停止.如图是他们离各自出发地的距离y(千米)与甲行驶时间x(小时)之间的函数关系图象,请结合图象信息,解答下列问题: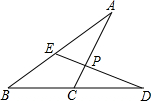 如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数.
如图所示,已知∠A=20°,∠B=30°,AC⊥DE,求∠BED和∠D的度数.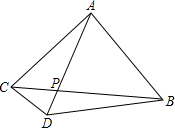 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求: