题目内容
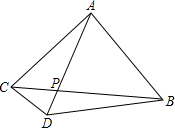 如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
如图所示,在△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:(1)∠BDC的度数,
(2)△ABD的周长.
考点:等腰三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)由条件可求得∠DAB=60°,结合等腰三角形的性质和三角形内角和定理可求得∠CDA和∠ADB,可求得∠BDC的底度数;
(2)由条件可证明△ABD为等边三角形,可求得其周长.
(2)由条件可证明△ABD为等边三角形,可求得其周长.
解答:解:(1)∵∠CAD=30°,AC=AD,
∴∠CDA=∠DCA=
(180°-30°)=75°,
又∵∠BAC=90°,∠CAD=30°,
∴∠DAB=60°,且AB=AD,
∴△ABD为等边三角形,
∴∠ADB=60°,
∴∠BDC=∠CDA+∠ADB=75°+60°=135°;
(2)由(1)可知△ABD为等边三角形,
∴AD=AB=BD=AC=6,
∴△ABD的周长为18.
∴∠CDA=∠DCA=
| 1 |
| 2 |
又∵∠BAC=90°,∠CAD=30°,
∴∠DAB=60°,且AB=AD,
∴△ABD为等边三角形,
∴∠ADB=60°,
∴∠BDC=∠CDA+∠ADB=75°+60°=135°;
(2)由(1)可知△ABD为等边三角形,
∴AD=AB=BD=AC=6,
∴△ABD的周长为18.
点评:本题主要考查等腰三角形的性质及等边三角形的判定和性质,由条件证明△ABD为等边三角形是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
直线m外的一点P,它到直线m上三点A,B,C的距离分别是6cm,3cm,5cm,则点P到直线m的距离为( )
| A、3cm | B、5cm |
| C、6cm | D、不大于3cm |
 已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.
已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.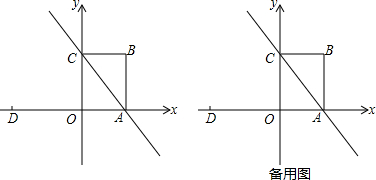
 如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.
如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式. 如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).
如图,已知坐标系中点A(2,-1),B(7,-1),C(3,-3).