题目内容
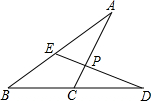如图所示，已知∠A=20°，∠B=30°，AC⊥DE，求∠BED和∠D的度数．考点：三角形的外角性质,三角形内角和定理
专题：
分析：根据垂直的定义可得∠APE=90°，然后利用三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠A+∠APE，然后利用三角形的内角和定理列式计算即可求出∠D．
解答：解：∵AC⊥DE，
∴∠APE=90°，
∴∠BED=∠A+∠APE=20°+90°=110°；
在△BDE中，∠D=180°-∠B-∠BED=180°-20°-110°=50°．
∴∠APE=90°，
∴∠BED=∠A+∠APE=20°+90°=110°；
在△BDE中，∠D=180°-∠B-∠BED=180°-20°-110°=50°．
点评：本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，三角形的内角和定理，熟记性质并准确识图是解题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图，已知AB是⊙O的直径，点C是⊙O外一点，连接CA，连接OC交⊙O于点F，交⊙O的弦AD于点E，若点E恰好是AD的中点，且∠C=∠DFB，试判断直线AC与⊙O的位置关系，并说明理由．
如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B作⊙O的切线交OP的延长线于点C．
如图，一次函数y=-