题目内容
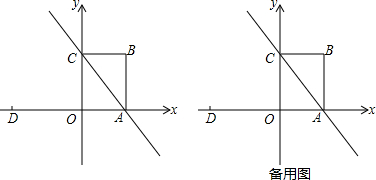
 求阴影部分面积.
求阴影部分面积.考点:扇形面积的计算
专题:
分析:构造图2,得到图1中的S1、S2、S3、S4,与图2中的S1、S2、S3、S4相等,易求得图2中S1+S2+S3+S4的值,得到图1中的阴影为
-(S1+S2+S3+S4).
| 90π(2a)2 |
| 360 |
解答: 解:如图:图1中的S1、S2、S3、S4,与图2中的S1、S2、S3、S4相等,
解:如图:图1中的S1、S2、S3、S4,与图2中的S1、S2、S3、S4相等,
由图2可知:S1+S2+S3+S4
=(2a)2-πa2
=4a2-πa2,
图1中的阴影为
-(S1+S2+S3+S4)=πa2-(4a2-πa2)=2πa2-4a2.
 解:如图:图1中的S1、S2、S3、S4,与图2中的S1、S2、S3、S4相等,
解:如图:图1中的S1、S2、S3、S4,与图2中的S1、S2、S3、S4相等,由图2可知:S1+S2+S3+S4
=(2a)2-πa2
=4a2-πa2,
图1中的阴影为
| 90π(2a)2 |
| 360 |
点评:本题考查了图形面积的计算,利用图形的等面积变换可以简化计算.

练习册系列答案
相关题目
直线m外的一点P,它到直线m上三点A,B,C的距离分别是6cm,3cm,5cm,则点P到直线m的距离为( )
| A、3cm | B、5cm |
| C、6cm | D、不大于3cm |

 如图,点C是线段AB的中点,BC=2BD,AB=4cm,求线段AD的长度.
如图,点C是线段AB的中点,BC=2BD,AB=4cm,求线段AD的长度.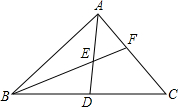 若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=
若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC= 如图,已知AB是⊙O的直径,点C是⊙O外一点,连接CA,连接OC交⊙O于点F,交⊙O的弦AD于点E,若点E恰好是AD的中点,且∠C=∠DFB,试判断直线AC与⊙O的位置关系,并说明理由.
如图,已知AB是⊙O的直径,点C是⊙O外一点,连接CA,连接OC交⊙O于点F,交⊙O的弦AD于点E,若点E恰好是AD的中点,且∠C=∠DFB,试判断直线AC与⊙O的位置关系,并说明理由. 有两个长为
有两个长为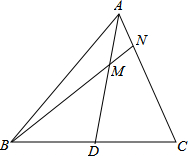 △ABC中,AD是中线,过B作直线交AD,AC于M,N且NA=NM,求证:BM=AC.
△ABC中,AD是中线,过B作直线交AD,AC于M,N且NA=NM,求证:BM=AC.