题目内容
8.矩形的周长20cm,两条对角线交于点0,过点0作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为多少.分析 由矩形的性质得出OA=OC,AB=CD,AD=BC,AD+CD=10cm,根据线段垂直平分线的性质,可得AE=CE,继而可得△CDE的周长等于AD+CD.
解答 解:如图所示: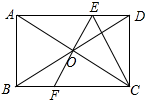
∵四边形ABCD是矩形,
∴OA=OC,AB=CD,AD=BC,
∵矩形的周长20cm,
∴AD+CD=10cm,
∵OE⊥AC,
∴AE=CE,
∴△CDE的周长为:CD+CE+DE=CD+CE+AE=AD+CD=10cm.
点评 此题考查了矩形的性质,线段垂直平分线的性质;根据线段垂直平分线的性质得出△CDE的周长=AD+CD是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资.每位销售人员的月销售定额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资.
(1)已知销售员甲本月分领到的工资总额为800元,请问甲本月的销售额为多少元?
(2)若销售员乙本月得到工资1300元,问乙本月的销售额为多少元?
(3)在(2)的条件下,已知乙本月销售A、B两种型号的彩电21台,且A型彩电的销售价为每台1000元,B型彩电的销售价为每台1500元,问乙本月销售A型彩电多少台?
(1)已知销售员甲本月分领到的工资总额为800元,请问甲本月的销售额为多少元?
(2)若销售员乙本月得到工资1300元,问乙本月的销售额为多少元?
(3)在(2)的条件下,已知乙本月销售A、B两种型号的彩电21台,且A型彩电的销售价为每台1000元,B型彩电的销售价为每台1500元,问乙本月销售A型彩电多少台?
| 销售额 | 奖励工资比例 |
| 超过0元但不超过5千元部分 | 5% |
| 超过0.5万元但不超过1万元部分 | 8% |
| 1万元以上的部分 | 10% |
7.若二次根式$\sqrt{\frac{1}{3-2a}}$有意义,则字母a应满足的条件是( )
| A. | $a<\frac{3}{2}$ | B. | $a≤\frac{3}{2}$ | C. | $a>\frac{3}{2}$ | D. | $a≥\frac{3}{2}$ |
8.一次函数y=-x+1的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
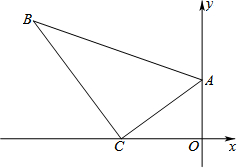 如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
如图,一块直角三角板ABC放置在平面直角坐标系中,∠B=30°,顶点A的坐标为(0,6),直角顶点C的坐标为(-8,0).
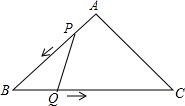 已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:
已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题: