题目内容
10.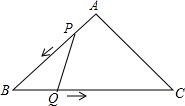 已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:
已知:如图,△ABC是等腰直角三角形,∠A=90°,AB=AC=3cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,P的速度是1cm/s,Q的速度是$\sqrt{2}$cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).解答下列问题:(1)当t为何值时,△PBQ是直角三角形?
(2)问:是否存在某一时刻t,使四边形APQC的面积与△PBQ面积差最小?如果存在,求出相应的t值;不存在,说明理由;
(3)设PQ的长为y(cm),试确定y与t之间的关系式;写出当t分别为何值时,PQ达到最短和最长,并写出PQ的最小值和最大值.
分析 (1)由于Rt△PBQ的直角不确定,需分∠BPQ=90°和∠BQP=90°两种情况讨论.由于∠B=45°,因此斜边是直角边的$\sqrt{2}$倍,由此建立关于t的等量关系,就可解决问题.
(2)分两种情况:①当0<t≤1时,作QM⊥AB于M,证出△BQM是等腰直角三角形,求出△PBQ的面积,得出四边形APQC的面积-△PBQ的面积是t的二次函数,即可得出结果;
②当t>1时,作PM⊥AB于M,同①得出四边形APQC的面积-△PBQ的面积是t的二次函数,即可得出结果;
(3)由勾股定理得出二次函数,即可得出PQ的最小值;当P到达B是,Q恰好到达C,即可得出结果.
解答 解:(1)由题可得:∠A=90°,AB=BC=4,∠B=45°,BQ=AP=t,BP=4-t.
①当∠PQB=90°时,如图1, ∵∠B=45°,
∵∠B=45°,
∴BQ=PQ,
∴BP=$\sqrt{2}$BQ.
∴3-t=$\sqrt{2}$•$\sqrt{2}$t,
解得:t=1;
②当∠BPQ=90°时,如图2, 同理可得:BQ=$\sqrt{2}$BP,
同理可得:BQ=$\sqrt{2}$BP,
∴$\sqrt{2}$t=$\sqrt{2}$(3-t),
解得:t=$\frac{3}{2}$;
综上所述;当t为1秒或$\frac{3}{2}$秒时,△PBQ是直角三角形.
(2)分两种情况:
①当0<t≤1时,作QM⊥AB于M,如图3所示:
∵∠B=45°,
∴△BQM是等腰直角三角形,
∴QM=BM=$\frac{\sqrt{2}}{2}$BQ=t,
∴△PBQ的面积=$\frac{1}{2}$BP•QM=$\frac{1}{2}$×(3-t)×t=$\frac{3}{2}$t-$\frac{1}{2}$t2,
∴四边形APQC的面积=△ABC的面积-△PBQ的面积=$\frac{1}{2}$×3×3-($\frac{3}{2}$t-$\frac{1}{2}$t2)=$\frac{1}{2}$t2-$\frac{3}{2}$t+$\frac{9}{2}$,
∴四边形APQC的面积-△PBQ的面积=t2-3t+$\frac{9}{2}$=(t-$\frac{3}{2}$)2+$\frac{9}{4}$,当t=$\frac{3}{2}$时,面积差最小,
但是t=$\frac{3}{2}$>1,不符合题意;
②当t>1时,作PM⊥AB于M,如图4所示:
∵∠B=45°,
∴△BPM是等腰直角三角形,
∴PM=BM=$\frac{\sqrt{2}}{2}$BP=$\frac{\sqrt{2}}{2}$(3-t),
∴△PBQ的面积=$\frac{1}{2}$BQ•PM=$\frac{1}{2}$×$\sqrt{2}$t×$\frac{\sqrt{2}}{2}$(3-t)=$\frac{3}{2}$t-$\frac{1}{2}$t2,
∴四边形APQC的面积=△ABC的面积-△PBQ的面积=$\frac{1}{2}$×3×3-($\frac{3}{2}$t-$\frac{1}{2}$t2)=$\frac{1}{2}$t2-$\frac{3}{2}$t+$\frac{9}{2}$,
∴四边形APQC的面积-△PBQ的面积=t2-3t+$\frac{9}{2}$=(t-$\frac{3}{2}$)2+$\frac{9}{4}$,当t=$\frac{3}{2}$时,面积差最小;
因此,存在某一时刻t,使四边形APQC的面积与△PBQ面积差最小,t=$\frac{3}{2}$秒;
(3)根据题意得:1≤t≤$\frac{3}{2}$时,存在t的值,使PQ最短,t=$\frac{6}{5}$;理由如下:
如图3所示:PM=3-2t,QM=t,
由勾股定理得:PQ2=PM2+QM2=(3-2t)2+t2=5t2-12t+9=5(t-$\frac{6}{5}$)2+$\frac{9}{5}$,
∴当t=$\frac{6}{5}$时,PQ2最小=$\frac{9}{5}$,
∴PQ的最小值=$\sqrt{\frac{9}{5}}$=$\frac{3\sqrt{5}}{5}$,
当t=1时,PQ=$\sqrt{2}$>$\frac{3\sqrt{5}}{5}$;
当t=$\frac{3}{2}$时,PQ=$\frac{3}{2}$$\sqrt{2}$>$\frac{3\sqrt{5}}{5}$;
综上所述:当t=$\frac{6}{5}$秒时,PQ最短,最小值=$\frac{3\sqrt{5}}{5}$;
当P到达B是,Q恰好到达C,此时t=3秒,PQ的最大值=BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
点评 本题考查了等腰直角三角形的判定与性质、勾股定理、三角形面积的计算等知识;本题综合性强,难度较大,需要通过作辅助线进行分类讨论才能得出结果.

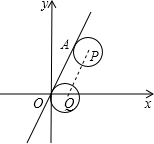 如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )
如图,在平面直角坐标系中,直线l经过原点以及点A(1,$\sqrt{3}$),圆P与直线l相切于点A,若圆P沿直线l滚动一周,点A恰好与原点重合,此时圆心位于点Q,则点Q的坐标为( )| A. | ($\frac{1}{2π},-\frac{\sqrt{3}}{π}$) | B. | ($\frac{1}{π},-\frac{\sqrt{3}}{π}$) | C. | ($\frac{\sqrt{3}}{2},-\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2π},-\frac{1}{2π}$) |
| A. | $\sqrt{36}=±6$ | B. | $4\sqrt{2}÷2\sqrt{2}$=$2\sqrt{2}$ | C. | $8\sqrt{3}-2\sqrt{6}$=6 | D. | $\sqrt{a}•\sqrt{b}=\sqrt{ab}$(a≥0,b≥0) |
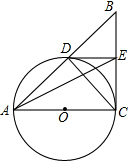 以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点.
以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于D,E是另一条直角边BC的中点. 如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.
如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.