题目内容
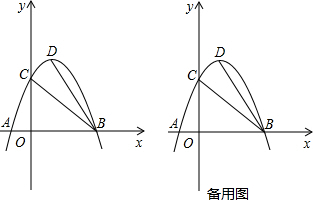
3.如图,抛物线y=-x2+2x+3与x轴交于点AB,与y轴交于点C,点D是抛物线的顶点,连接BC、BD.(1)点A的坐标是(-1,0),点B的坐标是(3,0),点D的坐标是(1,4);
(2)若点E是x轴上一点,连接CE,且满足∠ECB=∠CBD,求点E坐标;
(3)若点P在x轴上且位于点B右侧,点A、Q关于点P中心对称,连接QD,且∠BDQ=45°,求点P的坐标(请利用备用图解决问题)
分析 (1)令抛物线y=0,解方程可求点A的坐标和点B的坐标,根据抛物线的顶点式,可得抛物线的顶点坐标;
(2)根据待定系数法,可得BD的解析式,根据平行线的判定和两平行直线的函数解析式的关系,根据待定系数法,可得CE的解析式,进一步可得答案;
(3)根据勾股定理,可得BD的长,根据相似三角形的判定与性质,可得QN与BN的关系,根据等腰直角三角形的性质,可得DN与QN的关系,根据勾股定理,可得BQ的长,根据线段的和差,可得AQ的长,根据线段中点的性质,可得AP的长,根据线段的差,可得OP的长,可得P点坐标.
解答 解:(1)令抛物线y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
则点A的坐标是(-1,0),点B的坐标是(3,0),
y=-x2+2x+3=-(x-1)2+4,
则顶点D的坐标为(1,4).
故答案为:(-1,0),(3,0),(1,4);
(2)设BD所在直线的解析式为:y=k(x-3),将D点坐标代入函数解析式,得
-2k=4,
解得k=-2,
故BD所在直线的解析式为:y=-2x+6,
∵∠ECB=∠CBD,
∴CE∥BD,
设CE所在直线的解析式为:y=-2x+b,将C点坐标代入函数解析式,得b=3,
故CE所在直线的解析式为:y=-2x+3,
当y=0时,x=1.5;
∴点E坐标(0,1.5);
(3)如图: ,
,
连接QD,作QN⊥DB,交DB的延长线于N,
设对称轴与x轴的交点为点H.
∵点D坐标是(1,4)
∴点H坐标是(1,0)
∴DH=4,BH=2,
∴在Rt△BDH中,BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=2$\sqrt{5}$,
又∵∠QNB=∠DHB,∠QBN=∠DBH,
∴△QBN∽△DBH,
∴$\frac{QN}{DH}$=$\frac{BN}{BH}$,
∴$\frac{QN}{BN}$=$\frac{DH}{BH}$=$\frac{4}{2}$=2,
∴QN=2BN.
又∵∠BDQ=45°,
∴在Rt△DNQ中,∠DQN=45°,
∴DN=QN=2BN,
∴BN=BD=2$\sqrt{5}$,
∴QN=4$\sqrt{5}$.
∴在Rt△QBN中,BQ=$\sqrt{B{N}^{2}+N{Q}^{2}}$=10.
∵AB=4,
∴AQ=AB+BQ=14.
∴AP=$\frac{1}{2}$AQ=7
OP=AP-AO=7-1=6,
∴P(6,0).
点评 本题考查了二次函数综合题,利用配方法得出顶点坐标;利用待定系数法得出BD的解析式是解题关键;利用相似三角形的判定与性质得出QN与BN的关系是解题关键,又利用了等腰直角三角形的性质得出QN的长,利用勾股定理得出BQ的长.

 名校课堂系列答案
名校课堂系列答案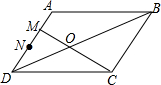 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
①不相交的直线叫做平行线;②两直线平行,同旁内角相等;③相等的角是对顶角;④过一点有且只有一条直线与已知直线垂直;⑤垂线段最短;⑥平方根等于本身的数是0和1;⑦邻补角是互补的角,这句话是一个假命题.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 120 | B. | 144 | C. | 196 | D. | 60 |
 某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分,
某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分, 如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.
如图,AB∥CD,∠A=50°,∠1-∠2=30°,求∠1的度数.