题目内容
10.(1)先化简,再求值:($\frac{{x}^{2}}{x-3}$+$\frac{9}{3-x}$)•$\frac{1}{{x}^{2}+3x}$,其中x=$\frac{1}{3}$;(2)计算并把结果用科学记数法表示:2.4×10-5÷(3×10-3).
分析 (1)先算括号里面的,再算乘法即可;
(2)根据同底数幂的乘法及除法法则进行计算即可.
解答 解:(1)原式=$\frac{(x+3)(x-3)}{x-3}$•$\frac{1}{x(x+3)}$
=$\frac{1}{x}$.
当x=$\frac{1}{3}$时,原式=3;
(2)原式=$\frac{2.4×{10}^{-5}}{3×{10}^{-3}}$
=8×10 -3.
点评 本题考查的是根与系数的关系,熟知x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.计算a7•($\frac{1}{a}$)2的结果是( )
| A. | a | B. | a5 | C. | a6 | D. | a8 |
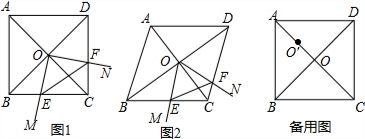
 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.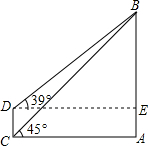 如图:某新电视塔,塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,求大楼的高度CD(结果精确到1米).
如图:某新电视塔,塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,求大楼的高度CD(结果精确到1米).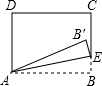 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.
如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.