题目内容
15. 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.
分析 连接DM,根据三角形的中位线定理得出EF=$\frac{1}{2}$DM,从而可知EF最大时,DM最大,因为M与B重合时DM最大,此时根据勾股定理求得DM=DB=6,从而求得EF的最大值为3.
解答  解:连接DM,
解:连接DM,
∵点E,F分别为MN,DN的中点,
∴EF=$\frac{1}{2}$DM,
∴DM最大时,EF最大,
∵M与B重合时DM最大,
此时DM=DB=$\sqrt{{AD}^{2}+{AB}^{2}}$=6,
∴EF的最大值为3.
故答案为:3.
点评 本题考查了三角形中位线定理,勾股定理的应用,熟练掌握定理是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
5.体育达标测试中,有8名男生“30秒跳绳”的成绩(单位:次)分别是:140,120,100,80,90,160,120,70,这组数据的中位数和众数分别是( )
| A. | 100,120 | B. | 120,110 | C. | 110,120 | D. | 120,120 |
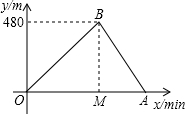 小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).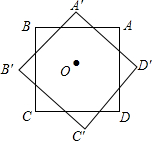 如图,已知正方形ABCD的边长为2,点O是正方形ABCD的中心,把正方形ABCD绕点O逆时针旋转45°得到正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分形成的正八边形的边长为2$\sqrt{2}$-2.
如图,已知正方形ABCD的边长为2,点O是正方形ABCD的中心,把正方形ABCD绕点O逆时针旋转45°得到正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分形成的正八边形的边长为2$\sqrt{2}$-2. 如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.
如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.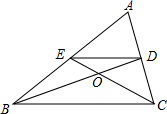 如图所示,DE是△ABC的中位线,BD与CE相交于点O,则$\frac{OB}{OD}$的值是2.
如图所示,DE是△ABC的中位线,BD与CE相交于点O,则$\frac{OB}{OD}$的值是2.