题目内容
20.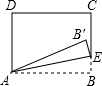 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.
如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.
分析 如图1,根据折叠的性质得到AB′=AB=5,B′E=BE,根据勾股定理得到BE2=(3-BE)2+12,
于是得到BE=$\frac{5}{3}$,如图2,根据折叠的性质得到AB′=AB=5,求得AB=BF=5,根据勾股定理得到CF=4根据相似三角形的性质列方程得到CE=12,即可得到结论.
解答 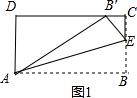 解:如图1,∵将△ABE沿AE折叠,得到△AB′E,
解:如图1,∵将△ABE沿AE折叠,得到△AB′E,
∴AB′=AB=5,B′E=BE,∴CE=3-BE,∵AD=3,∴DB′=4,∴B′C=1,∵B′E2=CE2+B′C2,
∴BE2=(3-BE)2+12,
∴BE=$\frac{5}{3}$,
如图2,∵将△ABE沿AE折叠,得到△AB′E,
∴AB′=AB=5,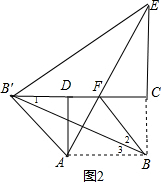
∵CD∥AB,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∵AE垂直平分BB′,
∴AB=BF=5,
∴CF=4,
∵CF∥AB,
∴△CEF∽△ABE,
∴$\frac{CF}{AB}=\frac{CE}{BE}$,
即$\frac{4}{5}$=$\frac{CE}{CE+3}$,
∴CE=12,∴BE=15,
综上所述:BE的长为:$\frac{5}{3}$或15,
故答案为:$\frac{5}{3}$或15.
点评 本题考查了翻折变换-折叠的性质,矩形的性质,平行线的性质,正确的作出图形是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
11. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )| A. | AO=OD | B. | AO⊥OD | C. | AO=OC | D. | AO⊥AB |
5.体育达标测试中,有8名男生“30秒跳绳”的成绩(单位:次)分别是:140,120,100,80,90,160,120,70,这组数据的中位数和众数分别是( )
| A. | 100,120 | B. | 120,110 | C. | 110,120 | D. | 120,120 |
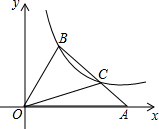 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.