题目内容

19．若两个相似三角形的相似比是1：2，则它们的面积比是1：4．

分析 利用似三角形的面积的比等于相似比的平方求解．

解答 解：因为两个相似三角形的相似比是1：2，
所以它们的面积比是1：4．
故答案为1：4．

点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的面积的比等于相似比的平方．

练习册系列答案
相关题目
9．计算：1-2sin30°=0．
10．（1）先化简，再求值：（$\frac{{x}^{2}}{x-3}$+$\frac{9}{3-x}$）•$\frac{1}{{x}^{2}+3x}$，其中x=$\frac{1}{3}$；
（2）计算并把结果用科学记数法表示：2.4×10-5÷（3×10-3）．
7．解方程：
（1）$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$；
（2）（x-2）2=2x-4．
14．3x2可以表示为（　　）
A．x2+x2+x2B．x2•x2•x2C．3x•3xD．9x
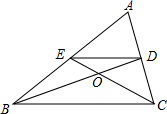4．如图所示，DE是△ABC的中位线，BD与CE相交于点O，则$\frac{OB}{OD}$的值是2．
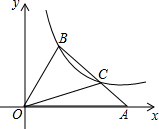11．如图，平行四边形ABCD的对角线AC、BD相交于点O，则下列说法一定正确的（　　）
A．AO=ODB．AO⊥ODC．AO=OCD．AO⊥AB
8．如图，在平面直角坐标系xOy中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B，C在反比例函数y=$\frac{2}{x}$（x＞0）的图象上，则△OAB的面积等于3．
9．计算$（\frac{1}{m}-1）÷\frac{{1-{m^2}}}{m}$的结果为$\frac{1}{m+1}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网