Question

2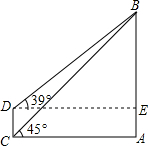．如图：某新电视塔，塔高AB为600米，远处有一栋大楼，某人在楼底C处测得塔顶B的仰角为45°，在楼顶D处测得塔顶B的仰角为39°，求大楼的高度CD（结果精确到1米）．
（参考数据：sin39°=cos51°≈0.630，cos39°=sin51°≈0.777，tan39°≈0.810，tan51°≈1.235）

Answer 1

分析 根据题意得到△BAC为等腰直角三角形，即可求出AC的长，设AE=DC=x米，在Rt△DEB中，根据tan39°=$\frac{BE}{DE}$求出x，即可求出CD的长．

解答 解：∵塔顶B的仰角为45°，
∴∠ABC=∠ACB=45°，
∴AC=AB=610米；
根据题意可知四边形ACDE为矩形，
则AC=DE，设AE=DC=x米，
则BE=（610-x）米，
在Rt△DEB中，tan39°=$\frac{BE}{DE}$，
∴$\frac{610-x}{610}$≈0.81，
解得x≈116．
答：大楼的高CD约为116米．

点评 本题考查了解直角三角形的应用---仰角俯角问题，熟悉等腰三角形的性质和三角函数的定义是解题的关键．