题目内容
20.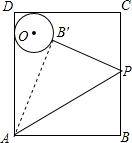 如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.
如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.
分析 连接OB′,作OH⊥BC于H,于是得到OH=DC-r=20-5=15,设BP=x,根据切线的性质得到∠OB′A=90°,由折叠的性质得到∠AB′P=∠B=90°,B′P=BP=x,推出O,B′,P共线,根据勾股定理列方程即可得到结论.
解答 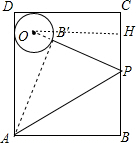 解:连接OB′,作OH⊥BC于H,
解:连接OB′,作OH⊥BC于H,
则OH=DC-r=20-5=15,
设BP=x,
∵AB′与⊙O相切于B′,
∴∠OB′A=90°,
由折叠的性质知:∠AB′P=∠B=90°,B′P=BP=x,
∴O,B′,P共线,
∴OP=OB′+B′P=x+5,
在Rt△OPH中,OH2+HP2=OP2,即152+(20-x)2=(x+5)2,
解得:x=12,
∴BP=12,
故答案为12.
点评 此题考查的知识点是切线的性质、矩形的性质即折叠的性质,勾股定理,根据勾股定理列方程是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
10.某灯泡厂生产节能灯泡1000只,其中有5只是次品,如果从中任取1只,这只灯泡是次品的概率是( )
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{500}$ | C. | $\frac{1}{200}$ | D. | $\frac{95}{1000}$ |
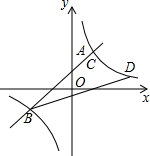 如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.
如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.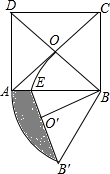 如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.