题目内容
13. 一、阅读理解:
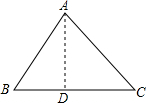
一、阅读理解:在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
分析 一、(1)由勾股定理即可得出结论;
(2)作AD⊥BC于D,则BD=BC-CD=a-CD,由勾股定理得出AB2-BD2=AD2,AC2-CD2=AD2,得出AB2-BD2=AC2-CD2,整理得出a2+b2=c2+2a•CD,即可得出结论;
(3)作AD⊥BC于D,则BD=BC+CD=a+CD,由勾股定理得出AD2=AB2=BD2,AD2=AC2-CD2,得出AB2-BD2=AC2-CD2,整理即可得出结论;
二、分两种情况:①当∠C为钝角时,由以上(3)得:$\sqrt{{a}^{2}+{b}^{2}}$<c<a+b,即可得出结果;②当∠B为钝角时,得:b-a<c<$\sqrt{{b}^{2}-{a}^{2}}$,即可得出结果.
解答 一、解:(1)∵∠C为直角,BC=a,CA=b,AB=c,
∴a2+b2=c2;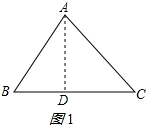
(2)作AD⊥BC于D,如图1所示:
则BD=BC-CD=a-CD,
在△ABD中,AB2-BD2=AD2,
在△ACD中,AC2-CD2=AD2,
∴AB2-BD2=AC2-CD2,
∴c2-(a-CD)2=b2-CD2,
整理得:a2+b2=c2+2a•CD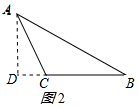
∵a>0,CD>0,
∴a2+b2>c2;
(3)作AD⊥BC于D,如图2所示:
则BD=BC+CD=a+CD,
在△ABD中,AD2=AB2-BD2,
在△ACD中,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,
∴c2-(a+CD)2=b2-CD2,
整理得:a2+b2=c2-2a•CD,
∵a>0,CD>0,
∴a2+b2<c2;
二、解:当∠C为钝角时,由以上(3)得:$\sqrt{{a}^{2}+{b}^{2}}$<c<a+b,
即5<c<7;
当∠B为钝角时,得:b-a<c<$\sqrt{{b}^{2}-{a}^{2}}$,
即1<c<$\sqrt{7}$;
综上所述:第三边c的取值范围为5<c<7或1<c<$\sqrt{7}$.
点评 本题考查了勾股定理的综合运用、完全平方公式;熟练掌握勾股定理,通过作辅助线运用勾股定理是解决问题的关键.

| A. | 扩大4倍 | B. | 扩大2倍 | C. | 不变 | D. | 缩小2倍 |
 在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2. 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向25海里的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,再向南偏东53°方向航行,同时捕鱼船向正北方向低速航行.若两船航速不变,并且在D处会合,求CD两点的距离和捕鱼船的速度(结果保留整数).
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向25海里的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,再向南偏东53°方向航行,同时捕鱼船向正北方向低速航行.若两船航速不变,并且在D处会合,求CD两点的距离和捕鱼船的速度(结果保留整数).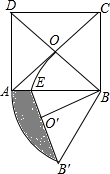 如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.