��Ŀ����
13��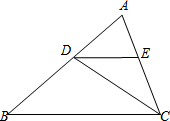 ��ͼ��ʾ����֪��ABC�У�AB=2��D��AB�����ƶ�������A��B�غϣ���DE��BC��AC��E����CD����S��ABC=S��S��DEC=S1��
��ͼ��ʾ����֪��ABC�У�AB=2��D��AB�����ƶ�������A��B�غϣ���DE��BC��AC��E����CD����S��ABC=S��S��DEC=S1����1����DΪAB�е�ʱ����S1��S��ֵ��
��2����AD=x��$\frac{{S}_{1}}{S}$=y������x�Ĵ���ʽ��ʾy������x��ȡֵ��Χ��
��3���Ƿ���ڵ�D��ʹ��S1��$\frac{1}{2}$S�����������ڣ������D��λ�ã��������ڣ���˵�����ɣ�
���� ��1����DΪAB�е�ʱ��DE��������ABC����λ�ߣ�DE��BC=1��2�������ߵı�Ҳ��1��2���������ε�����ıȾͿ��������
��2���������������ε����ʣ����Եõ��ױ�DE��BC�Լ�����֮��Ĺ�ϵ���Ϳ����������ıȣ�
��3��ʹ��S1��$\frac{1}{2}$S����������ת��Ϊ����ֵy�Ĵ�С��ϵ��
��� �⣺��ͼ��
��A��AM��BC����DE�ڵ�N����AD=x��
��DE��BC��
��$\frac{DE}{BC}=\frac{AN}{AM}=\frac{AD}{AB}=\frac{x}{2}$��
��DE=$\frac{x}{2}$��BC��AN=$\frac{x}{2}$��AM��
��1����DΪAB�е�ʱ��DE��������ABC����λ�ߣ�
��DE=$\frac{1}{2}$BC��AN=$\frac{1}{2}$AM��
��S��ABC=S=$\frac{1}{2}$AM��BC��
��S��DEC=S1=$\frac{1}{2}$AN��DE��
��$\frac{{S}_{1}}{S}=\frac{\frac{1}{2}AN��DE}{\frac{1}{2}AM��BC}=\frac{\frac{1}{2}��\frac{1}{2}AM��\frac{1}{2}BC}{\frac{1}{2}AM��BC}=\frac{1}{4}$��
��2����DE��BC��
��$\frac{DE}{BC}=\frac{AN}{AM}=\frac{AD}{AB}=\frac{x}{2}$��
��$\frac{NM}{AM}=\frac{2-x}{2}$��
��$\frac{{S}_{1}}{S}=\frac{\frac{1}{2}MN��DE}{\frac{1}{2}AM��BC}$=$\frac{DE}{BC}$��$\frac{NM}{AM}$=$\frac{x}{2}$��$\frac{2-x}{2}$=$\frac{{-x}^{2}+2x}{4}$��
��y=-$\frac{1}{4}$x2+$\frac{x}{2}$��0��x��2����
��3�������ڵ�D��ʹS1��$\frac{1}{2}$S��
�������£�
������ڵ�D��ʹS1��$\frac{1}{2}$S��
��$\frac{{S}_{1}}{S}��\frac{1}{2}$��
��y��$\frac{1}{2}$��
��$\frac{{-x}^{2}+2x}{4}��\frac{1}{2}$��
�ࣨx-1��2��-1��
����x-1��2��0��
��x�����ڣ�
�����ڵ�D��ʹS1��$\frac{1}{2}$S��
���� �������������ۺ��⣬��Ҫ���������������ε����ʣ��Լ������ε�����ļ��㷽����

 ��У����ϵ�д�
��У����ϵ�д�| ������� | Ů�� | ���� |
| ������� | 20 | 27 |
| ���������� | 18 | 24 |
| ������ | 12 | 9 |
��2�������У�ÿ�������������ռ�ٷ�֮����Ȼ����ݼ��������������μ������������������ͳ��ͼ��
 ��ƽ��ֱ������ϵ�У�ֱ��y=-x+2�뷴��������y=$\frac{1}{x}$��ͼ����Ψһ�����㣬��ֱ��y=-x+b�뷴��������y=$\frac{1}{x}$��ͼ����2�������㣬��b��ȡֵ��Χ��b��2��b��-2��
��ƽ��ֱ������ϵ�У�ֱ��y=-x+2�뷴��������y=$\frac{1}{x}$��ͼ����Ψһ�����㣬��ֱ��y=-x+b�뷴��������y=$\frac{1}{x}$��ͼ����2�������㣬��b��ȡֵ��Χ��b��2��b��-2��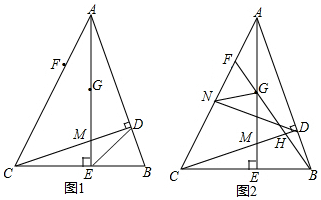
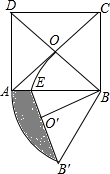 ��ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB�Ƶ�B��ʱ����ת60��õ���BO��B�䣬AB�뻡OO���ཻ�ڵ�E����AD=2����ͼ����Ӱ���ֵ������$\frac{2��}{3}$-$\frac{\sqrt{6}}{2}$��
��ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB�Ƶ�B��ʱ����ת60��õ���BO��B�䣬AB�뻡OO���ཻ�ڵ�E����AD=2����ͼ����Ӱ���ֵ������$\frac{2��}{3}$-$\frac{\sqrt{6}}{2}$��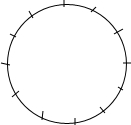 ���꼶��3����48�˲μӿ�������16�˴�����8�˴�ƹ����4��������12�˴����������˲μӳ��ܣ�������ͼ��ʮ���ȷֵ�Բ���ϣ�������ͳ��ͼ��ʾѧ���μӿ����������
���꼶��3����48�˲μӿ�������16�˴�����8�˴�ƹ����4��������12�˴����������˲μӳ��ܣ�������ͼ��ʮ���ȷֵ�Բ���ϣ�������ͳ��ͼ��ʾѧ���μӿ����������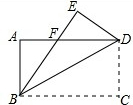 ��ͼ��������ֽƬABCD�ضԽ���BD�۵�����C���ڵ�E����BE��AD�ڵ�F����֤��AF=EF��
��ͼ��������ֽƬABCD�ضԽ���BD�۵�����C���ڵ�E����BE��AD�ڵ�F����֤��AF=EF��