题目内容
14.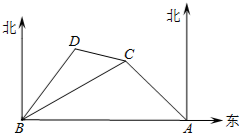 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.(参考数据:sin38°≈$\frac{3}{5}$,tan22°≈$\frac{2}{5}$,tan37°≈$\frac{3}{4}$)
(1)求BC的距离.
(2)求CD的距离.
分析 (1)作CE⊥AB于E,根据正弦的定义求出CE的长,根据直角三角形的性质求出BC的长;
(2)作DF⊥BC于F,设DF=xkm,根据正切的定义用x表示出CF、BF,结合图形计算即可求出x的值,根据勾股定理计算即可.
解答 解:(1) 作CE⊥AB于E,
作CE⊥AB于E,
由题意得,∠CAE=45°,∠CBE=30°,
∴AE=CE=AC•sin∠CAE=23$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=23km,
∴BC=2CE=46km,
答:BC的距离为46km;
(2)作DF⊥BC于F,
设DF=xkm,
∴CF=$\frac{DF}{ran∠DCB}$=$\frac{4}{3}$x,
BF=$\frac{DF}{tan∠DBC}$=$\frac{5}{2}$x,
则$\frac{4}{3}$x+$\frac{5}{2}$x=46,
解得,x=12,
∴DF=12,CF=16,
由勾股定理得,CD=$\sqrt{D{F}^{2}+C{F}^{2}}$=20km.
答:CD的距离为20km.
点评 本题考查的是解直角三角形的应用-方向角问题,正确作出辅助线、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4.
如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4. △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,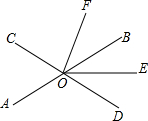 如图,直线AB,CD相交于点O,OE平分∠BOD.
如图,直线AB,CD相交于点O,OE平分∠BOD.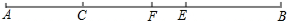 如图,已知线段AB=32,C为线段AB上一点,且AC=$\frac{1}{3}$BC,E为线段BC的中点,F为线段AB的中点,求线段EF的长.
如图,已知线段AB=32,C为线段AB上一点,且AC=$\frac{1}{3}$BC,E为线段BC的中点,F为线段AB的中点,求线段EF的长. 如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
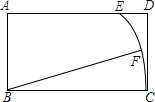 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.