题目内容
2.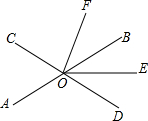 如图,直线AB,CD相交于点O,OE平分∠BOD.
如图,直线AB,CD相交于点O,OE平分∠BOD.(1)若∠EOF=55°,OD⊥OF,求∠AOC的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠DOE的度数.
分析 (1)利用角平分线的性质结合已知得出∠DOE的度数,进而得出答案;
(2)利用角平分线的性质结合已知表示出∠DOE、∠COF的度数,进而得出答案.
解答 解:(1)∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠EOF=55°,OD⊥OF,
∴∠DOE=35°,
∴∠BOE=70°,
∴∠AOC=70°;
(2)∵OF平分∠COE,
∴∠COF=∠EOF,
∵∠BOF=15°,
∴设∠DOE=∠BOE=x,
则∠COF=x+15°,
∴x+15°+x+15°+x=180°,
解得:x=50°,
故∠DOE的度数为:50°.
点评 此题主要考查了角平分线的性质,得出用同一未知数表示出各角度数是解题关键.

练习册系列答案
相关题目
10. 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )| A. | $60\sqrt{3}$ | B. | 61 | C. | $60\sqrt{3}+1$ | D. | 121 |
17.下列各组中,不是同类项的是( )
| A. | 32与23 | B. | -3ab与ba | C. | 0.2a2b与$\frac{1}{5}{a^2}b$ | D. | a2b3与-a3b2 |
7.多项式2x-3y+4+3kx+2ky-k中没有含y的项,则k应取( )
| A. | k=$\frac{3}{2}$ | B. | k=0 | C. | k=-$\frac{2}{3}$ | D. | k=4 |
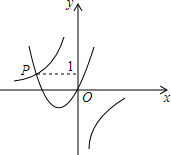 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.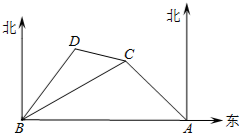 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2cm,则AB=4cm.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2cm,则AB=4cm.