题目内容
6．如图是单位长度为1的网格（1）在图1中画出一条长$\sqrt{5}$的线段；
（2）在图2中画出一个以格点为顶点，面积为10的等腰三角形．
分析 （1）由勾股定理得出$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，长$\sqrt{5}$的线段是直角边长为1，2的直角三角形的斜边；画出图形即可；
（2）让底边长为4，高为5的等腰三角形即可．
解答 解：
（1）由勾股定理得：
$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
长$\sqrt{5}$的线段如图1所示：
（2）∵$\frac{1}{2}$×4×5=10，
∴画底边长为4，高为5的等腰三角形，如图2所示：
点评 本题考查了勾股定理、等腰三角形的判定、三角形面积的计算；熟练掌握勾股定理和等腰三角形的性质是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．如图，将一副三角尺按不同位置摆放，∠α与∠β互余的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
17．下列各组中，不是同类项的是（ ）
| A． | 32与23 | B． | -3ab与ba | C． | 0.2a2b与$\frac{1}{5}{a^2}b$ | D． | a2b3与-a3b2 |
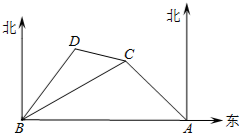2016年1月6日，我国南沙永暑礁新建港口、机场完成试航试飞，将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持，使航行和飞行更为安全可靠．如图所示，永暑礁新建港口在A处，位于港口A的正西方的有一小岛B，小岛C在小岛B的北偏东60°方向，小岛C在A的北偏西45°方向；小岛D在小岛B的北偏东38°方向且满足∠BCD=37°，港口A和小岛C的距离是23$\sqrt{2}$km．
1．
在Rt△ACB中，∠C=90°，BC=5，AC=12，则sinA=（ ）
在Rt△ACB中，∠C=90°，BC=5，AC=12，则sinA=（ ）| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{5}{13}$ | D． | $\frac{12}{13}$ |
如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=2cm，则AB=4cm．
2015年12月27当日上午8时42分，第一列“和谐号”动车驶入扬州火车站．已知动车的速度比普通客车的速度快70km/h，小路同学从扬州去A地游玩，本打算乘坐普通客车，需要2小时才能到达；由于得知开通了动车，决定乘坐动车，她发现乘坐动车比乘坐普通客车节约40分钟．求动车的速度和扬州与A地之间的距离．