题目内容
19.计算(1)${(-3)^2}-{(1\frac{1}{2})^3}×\frac{2}{9}-6÷|{-\frac{2}{3}}$|
(2)$[{-{3^4}-2\frac{1}{4}×(-4)}]÷(14\frac{9}{13}-16\frac{9}{13})$
(3)化简求值:$\frac{1}{2}$x-2(x-$\frac{1}{3}$y2)+(-$\frac{3}{2}$x+$\frac{1}{3}$y2),其中x=-2,y=-$\frac{2}{3}$.
分析 (1)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式先计算括号中的运算,再计算除法运算即可得到结果;
(3)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=9-$\frac{27}{8}$×$\frac{2}{9}$-6×$\frac{3}{2}$=9-$\frac{3}{4}$-9=-$\frac{3}{4}$;
(2)原式=(-81+9)÷(-2)=(-72)÷(-2)=36;
(3)原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2-$\frac{3}{2}$x+$\frac{1}{3}$y2=-3x+y2,
当x=-2,y=-$\frac{2}{3}$时,原式=6$\frac{4}{9}$.
点评 此题考查了有理数的混合运算,以及整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.下列命题中,真命题是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 顺次连接四边形的各边中点所得的四边形是平行四边形 | |
| D. | 两条对角线互相平分且相等的四边形是正方形 |
4. 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )| A. | AB=EF | B. | ∠E=∠B | C. | CD=AF | D. | ED=BC |
8.已知△ABC∽△DEF,其相似比为4:9,则△ABC与△DEF的面积比是( )
| A. | 2:3 | B. | 3:2 | C. | 16:81 | D. | 81:16 |
9.△ABC∽△DEF且它们的面积比为$\frac{9}{4}$,则周长比是( )
| A. | $\frac{81}{16}$ | B. | $\frac{3}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{2}{3}$ |
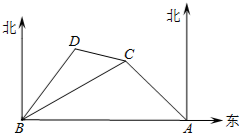 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.