题目内容
19. 如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
如图,直径AB、CD所夹锐角为60°,点P为$\widehat{BC}$上的一个动点(不与点B、C重合),PM、PN分别垂直于CD、AB,垂足分别为点M、N.若⊙O的半径为2cm,则在点P移动过程中,MN的长是否有变化否(填“是”或“否”),若有变化,写出MN的长度范围;若无变化,写出MN的长度:$\sqrt{3}$cm.
分析 因为P为⊙O上的一个动点(不与点A,B,C,D重合),所以可以考虑特殊情况下即当PN⊥AB于圆心O时,延长PN交圆与点E,PM⊥CD,延长PM交圆于点F,连接EF,求出EF的长,得到MN的长,根据圆周角、圆心角、弧、弦之间的关系得到答案.
解答 解:MN的长没有变化;理由如下: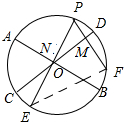
如图所示,当PN⊥AB于圆心O时,延长PN交圆与点E,PM⊥CD,延长PM交圆于点F,连接EF,
根据垂径定理,MN=$\frac{1}{2}$EF,
∵∠AOD=120°,PN⊥AB,
∴∠PNM=30°,∠P=60°,
在Rt△PEF中,PE=4,则EF=2$\sqrt{3}$
∴MN=$\sqrt{3}$,
点P移动时,由题意得:∠P=60°,
由垂径定理,始终有MN∥EF且MN=$\frac{1}{2}$EF,
即弦长为2$\sqrt{3}$,
∴MN=$\sqrt{3}$.
故答案为:否,$\sqrt{3}$.
点评 本题考查的是垂径定理、三角形中位线定理和锐角三角函数的运用,求出特殊情况下的MN的值是解题的关键,解答时,要灵活运用圆周角、圆心角、弧、弦之间的关系.

练习册系列答案
相关题目
10. 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )| A. | $60\sqrt{3}$ | B. | 61 | C. | $60\sqrt{3}+1$ | D. | 121 |
7.多项式2x-3y+4+3kx+2ky-k中没有含y的项,则k应取( )
| A. | k=$\frac{3}{2}$ | B. | k=0 | C. | k=-$\frac{2}{3}$ | D. | k=4 |
3. 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
4. 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )| A. | AB=EF | B. | ∠E=∠B | C. | CD=AF | D. | ED=BC |
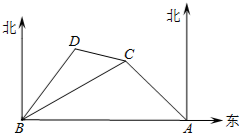 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km. 在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠ADE=50°,则∠B=70°.
在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠ADE=50°,则∠B=70°. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2cm,则AB=4cm.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2cm,则AB=4cm.