题目内容
3.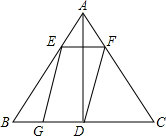 如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.
如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.
分析 由FE与BC平行,得到△AFE与△形ABC相似,根据相似三角形的性质即可得到结论,注意对重叠部分形状进行分类讨论.
解答 解:∵AB=AC=10,BC=12,AD⊥BC,
∴BD=$\frac{1}{2}$BC=6,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=8,
∴S△ABC=$\frac{1}{2}$×12×8=48,
∵?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$,
∴S四边形EFDG=$\frac{1}{3}×$48=16,
设AD,EF交于H,
∵FE∥BC,
∴△AFE∽△ABC,
∴$\frac{EF}{AH}=\frac{BC}{AD}$=$\frac{12}{8}$=$\frac{3}{2}$,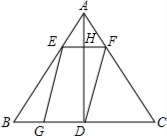 ∴AH=$\frac{2EF}{3}$,
∴AH=$\frac{2EF}{3}$,
∴HD=8-$\frac{2EF}{3}$,
①当重叠面积为平行四边形时(如图),
S重叠=S四边形EFDG=EF•DH=EF(8-$\frac{2EF}{3}$)=16,
∴EF=6-2$\sqrt{3}$(6+2$\sqrt{3}$不合题意,舍去),
②当重叠面积为梯形时(如图)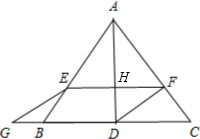
S重叠=S梯形EFDB=$\frac{(EF+BD)×HD}{2}$=16
解得EF=3+$\sqrt{33}$(3-$\sqrt{33}$不合题意,舍去);
故答案为:6-2$\sqrt{3}$或3+$\sqrt{33}$.
点评 本题考查了相似三角形的判定与性质,平行四边形的面积,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
15.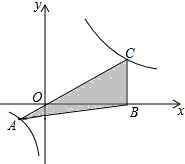 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
12.为提升城市品位,改善城市环境,2015年2月27日,许昌市护城河环通工程开工建设,时隔一年,“桨声欸乃乃何叶碧,一舟环游许昌城”的诗情画意已基本成为现实.据悉,全长约5公里的护城河总蓄水量达37万立方米,将数据37万用科学记数法表示为( )
| A. | 37×104 | B. | 3.7×104 | C. | 37×105 | D. | 3.7×105 |
18.若三角形三条边的长分别是7,24,25,则这个三角形的最大内角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |