题目内容
15.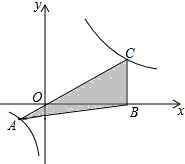 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
分析 设点A的坐标为(m,$\frac{1}{m}$),直线AC经过点A,可求得直线AC的表达式为y=$\frac{1}{{m}^{2}}$x.直线AC与函数y=$\frac{{k}^{2}}{x}$一个交点为点C,则可求得点C的坐标当k>0时C为(-mk,-$\frac{k}{m}$),故$\frac{1}{2}$×(-$\frac{k}{m}$)(-mk+|m|)=6,求出k的值即可.
解答 解:设A(m,$\frac{1}{m}$)(m<0),直线AC的解析式为y=ax(k≠0),
∵A(m,$\frac{1}{m}$),
∴ma=$\frac{1}{m}$,解得a=$\frac{1}{{m}^{2}}$,
∴直线AC的解析式为y=$\frac{1}{{m}^{2}}$x.
∵AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,
∴C(-mk,-$\frac{k}{m}$),
∵△ABC的面积等于6,CB⊥x轴,
∴$\frac{1}{2}$×(-$\frac{k}{m}$)(-mk+|m|)=6,解得k1=-4(舍去),k2=3.
故选C.
点评 本题考查的是反比例函数系数k的几何意义,根据题意得出直线AC的解析式,再用m表示出C点坐标是解答此题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
5.小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了$\frac{1}{4}$,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
| A. | $\frac{40}{x+20}$=$\frac{3}{4}$×$\frac{40}{x}$ | B. | $\frac{40}{x}$=$\frac{3}{4}×\frac{40}{x+20}$ | C. | $\frac{40}{x+20}$+$\frac{1}{4}$=$\frac{40}{x}$ | D. | $\frac{40}{x}$=$\frac{40}{x+2}$-$\frac{1}{4}$ |
6. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=$\frac{1}{2}$∠BCD,②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF中一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=$\frac{1}{2}$∠BCD,②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF中一定成立的是( )
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=$\frac{1}{2}$∠BCD,②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF中一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=$\frac{1}{2}$∠BCD,②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF中一定成立的是( )| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
10.据全国假日旅游协调会议办公室发布的报告显示,在今天中秋,国庆8天长假期间,全国共接待游客4.25亿人次,这个数字用科学记数法表示为( )
| A. | 4.25×109 | B. | 4.25×1010 | C. | 4.25×1011 | D. | 4.25×1012 |
7.下列命题正确的是( )
| A. | 如果两个角相等,那么这两个角是对顶角 | |
| B. | 直线外一点和直线上的点连线,垂线最短 | |
| C. | 平面内经过一点有且只有一条直线与已知直线平行 | |
| D. | 平面内经过一点有且只有一条直线与已知直线垂直 |
9.下列命题中正确的是( )
| A. | 周长相等的两个三角形全等 | |
| B. | 关于某条直线对称的两个三角形全等 | |
| C. | 顶角相等的两个等腰三角形全等 | |
| D. | 两边和一角对应相等的两个三角形全等 |
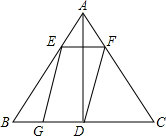 如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.
如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作?EFDG,当?EFDG与△ABC重叠部分为△ABC的面积的$\frac{1}{3}$时,线段EF的长为6-2$\sqrt{3}$或3+$\sqrt{33}$.